题目内容
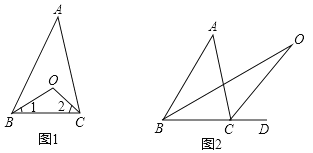
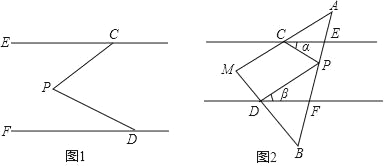
【题目】(问题探究)如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;
(问题迁移)
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
(1)当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.
(2)如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
【答案】【问题探究】∠DPC=α+β,理由详见解析;【问题迁移】(1)70;(2)∠DPC=β﹣α
【解析】
问题探究:延长CP交DF于A,根据平行线的性质以及三角形外角性质进行计算即可;
问题迁移:(1)延长CP交DF于G,根据平行线的性质以及三角形外角性质进行计算即可;
(2)分两种情况进行讨论:点P在BF上,点P在AE上,分别根据平行线的性质以及三角形外角性质进行计算即可.
问题探究:∠DPC=α+β.
理由:如图,延长CP交DF于A,
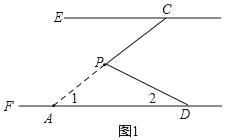
∵DF∥CE,
∴∠PCE=∠1=α,
∵∠DPC=∠2+∠1=180°﹣∠APD,
∴∠DPC=∠2+∠PCE=α+β;
问题迁移:(1)如图2,延长CP交DF于G,
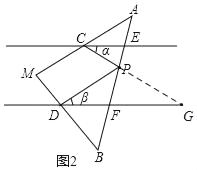
∵DF∥CE,
∴∠PCE=∠G=30°,
∴∠DPC=∠G+∠GDP=30°+40°=70°,
故答案为:70;
(2)如图,∠DPC=β﹣α
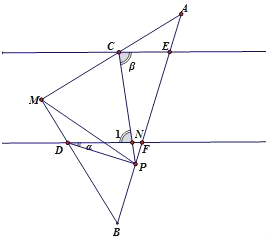
∵DF∥CE,
∴∠PCE=∠1=β,
∵∠DPC=∠1﹣∠FDP=∠1﹣α.
∴∠DPC=β﹣α;
如图,∠DPC=α﹣β
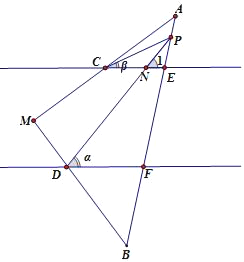
∵DF∥CE,
∴∠PDF=∠1=α,
∵∠DPC=∠1﹣∠ACE=∠1﹣β.
∴∠DPC=α﹣β.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ![]() ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表: 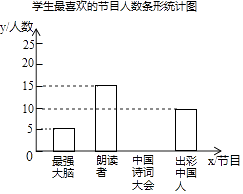
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
根据以上提供的信息,解答下列问题:
(1)x= , a= , b=;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
【题目】林丛同学调查了全班50名同学分别喜欢相声、小品、歌曲、舞蹈节目的情况,并制成下面的统计表:
最喜欢的节目类型 | 划记 | 人数 | 百分比 |
相声 | 正 | 13 | 26% |
小品 | 正正正一 | 21 | 42% |
歌曲 | 正正 | 10 | 28% |
舞蹈 | 正一 | 6 | 12% |
在上表所给的数据中,仅有一类节目的统计是完全正确的,则该项目统计类别是________.