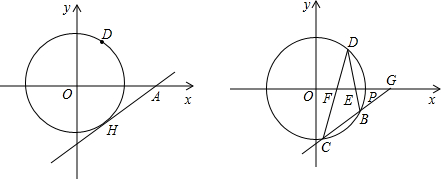题目内容
已知⊙O过点D(3,4),点H与点D关于x轴对称,过H作⊙O的切线交x轴于点A.
(1)求sin∠HAO的值;
(2)如图,设⊙O与x轴正半轴交点为P,点E、F是线段OP上的动点(与点P不重合),连接并延长DE、DF交⊙O于点B、C,直线BC交x轴于点G,若△DEF是以EF为底的等腰三角形,试探索sin∠CGO的大小怎样变化,请说明理由.

 解:(1)点D(3,4)在⊙O上,
解:(1)点D(3,4)在⊙O上,∴⊙O的半径r=OD=5;
如图,连接HD交OA于Q,则HD⊥OA,连接OH,则OH⊥AH,
∴∠HAO=∠OHQ,
∴sin∠HAO=sin∠OHQ=
 =
= ;
;(2)解:不变.
如图,设点D关于x轴的对称点为H,连接HD交OP于Q,则HD⊥OP,
又DE=DF,
∴DH平分∠BDC,
∴
 =
= .
.∴连接OH,则OH⊥BC,
在Rt△OKG与Rt△OHQ中,
∵∠OKG=∠OEH=90°,∠HOG=∠HOG,
∴∠CGO=∠OHQ,
∴sin∠CGO=sin∠OHQ=
 =
= ,
,所以不变.
分析:(1)因为点D在圆上,根据点D的坐标利用勾股定理即可求得OD的长,即半径;连接HD交OA于Q,则HD⊥OA,连接OH,则OH⊥AH,根据同角的余角相等可得到∠HAO=∠OHQ,根据已知可求得sin∠OHQ的值,则sin∠HAO的值也就求得了;
(2)设点D关于x轴的对称点为H,连接HD交OP于Q,则HD⊥OP,根据角平分线的性质及垂径定理可得到∠CGO=∠OHQ,则求得sin∠OHQ的值sin∠CGO也就求得了.
点评:此题主要考查学生对切线性质,关于x轴、y轴、原点对称点的坐标,解直角三角形及垂径定理等知识点的综合运用.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
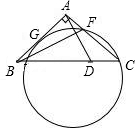 如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC.已知圆过点C且与AC相交于F,与AB相切于AB的中点G.求证:AD⊥BF.
如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC.已知圆过点C且与AC相交于F,与AB相切于AB的中点G.求证:AD⊥BF.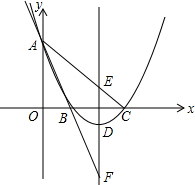 如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.