题目内容
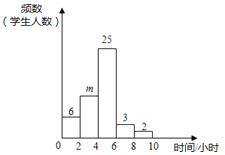
【题目】如图所示为一几何体的三视图．
(1)写出这个几何体的名称：____________；
(2)在虚线框中画出它的一种表面展开图；
(3)若主视图中长方形较长一边的长为5cm，俯视图中三角形的边长为2cm，则这个几何体的侧面积是________cm2.
【答案】详见解析.
【解析】试题分析：
(1) 观察题目中给出的三视图可以发现，该几何体上下底面是全等的等边三角形，侧面为全等的矩形. 根据这些几何特征可以判定该几何体为正三棱柱.
(2) 正三棱柱的上下底面为两个全等的等边三角形，侧面为三个全等的矩形. 在表面展开图中，中间部分应该是表示侧面的三个并行排列的矩形，这些矩形较短的边长应该为底面的边长，较长的边长应该为正三棱柱的高；在位于中间的矩形的上方和下方各有一个表示上下底面的等边三角形.
(3) 结合题目中给出的条件观察第(2)小题中得到的表面展开图可知，由已知条件可以求得展开图中部的三个矩形的面积. 根据正三棱柱的几何特征可知，其侧面积可以由这三个矩形的面积之和求得.
试题解析：
(1) 根据题目中给出的三视图的特征可知，该几何体为正三棱柱. 故本小题应填写：正三棱柱.
(2) 根据正三棱柱的几何特征，画出如下的表面展开图.
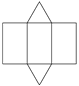
(3) 本小题应填写：30. 求解过程如下.
利用第(2)小题得到的正三棱柱表面展开图(如图)，计算几何体的侧面积.
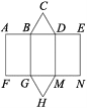
由题意可知，AF=BG=DM=EN=5cm，BC=BD=CD=2cm.
根据正三棱柱的几何特征可知：四边形ABGF，四边形BDMG，四边形DENM为全等的矩形.
∵矩形BDMG的面积为：
(cm2)，
∴矩形ABGF与矩形DENM的面积均为10cm2.
根据正三棱柱的几何特征可知，正三棱柱的侧面积等于四边形AENF的面积，即上述三个矩形面积之和，故该正三棱柱的侧面积应为：
(cm2).
阳光课堂课时优化作业系列答案
