��Ŀ����
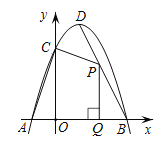
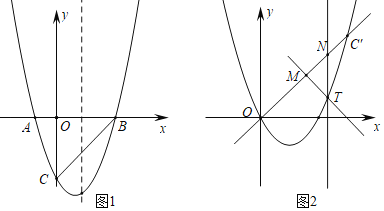
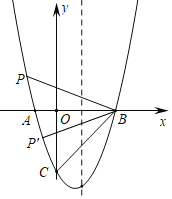
����Ŀ����ͼ1��������y��ax2+bx+c��x�ύ�ڵ�A(��1��0)��B(3��0)����y�ύ�ڵ�C(0����3).
(1)�������ߵĽ���ʽ��
(2)���������Ƿ����һ��P��ʹ�á�APB����ACO�����������ڣ������P�����꣺�������ڣ���˵������.
(3)���ǹ涨������ֱ��l1��y��k1x+b��ֱ��l2��y��k2x+b2����ֱ��k1k2����1����ֱ��l1��l2��������Ҳ����.���������涨������п��⣺
��ͼ2����������������ƽ�ƹ�ԭ����ֱ��y��kx(k��0)������C��.��TΪ�ö��κ���ͼ����λ��ֱ��OC�·��Ķ��㣬����T��ֱ��TM��OC��������Ϊ��M����M���߶�OC����(����O��C���غ�)������T��ֱ��TN��y�ύOC'�ڵ�N.���ڵ�T�˶��Ĺ����У�![]() Ϊ��������ȷ��k��ֵ.
Ϊ��������ȷ��k��ֵ.
���𰸡�(1)y��x2��2x��3��(2)���ڣ���P(��![]() ��
��![]() ��(��
��(��![]() ����
����![]() )��(3)k��
)��(3)k��![]() .
.
��������
(1)�����ߵı���ʽΪ��y��a(x+1)(x��3)��a(x2��2x��3)��������⣻
(2)�ֵ�P��x���Ϸ�����P��x���·�����������ֱ���⼴�ɣ�
(3)OM��![]() ��
��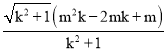 ��ON��m
��ON��m![]() ���������.
���������.
�⣺(1)�����ߵı���ʽΪ��y��a(x+1)(x��3)��a(x2��2x��3)��
����3a����3����ã�a��1��
�������ߵı���ʽΪ��y��x2��2x��3������
(2)tan��APB��tan��ACO��![]() ��
��
������P��x���Ϸ�ʱ��
��ֱ��BP�ı���ʽΪ��y����![]() x+1������
x+1������
�����٢�����ã�x��3(��ȥ)��![]() ���ʵ�P(��
���ʵ�P(��![]() ��
��![]() )��
)��
������P��x���·�ʱ��
ͬ���ɵã���P(��![]() ����
����![]() )��
)��
���ϣ���P(��![]() ��
��![]() ��(��
��(��![]() ����
����![]() )��
)��
(3)���T(m��m2��2m)��ֱ��ON�ı���ʽΪ��y��kx������
��TM��OC����ֱ��TMΪ��y����![]() x+b��
x+b��
����T�����������ʽ����ã�
ֱ��TM�ı���ʽΪ��y����![]() x+(m2��2m+
x+(m2��2m+![]() )������
)������
�����ۢ�����ã�x��![]() ��y��
��y��![]() ��
��
��OM��![]() ��
��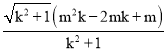 ��ON��m
��ON��m![]() ��
��
![]() ��
��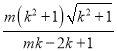 ��
��
��k��![]() ʱ��
ʱ��![]() ��
��![]() ����.
����.