题目内容
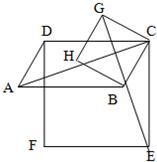23、如图，ABCD为平行四边形，DFEC和BCGH为正方形．求证：AC⊥EG．分析：本题中要证AC⊥EG也就是证∠CGE+∠GCA=90°，我们发现∠GBA+∠ACB=90°，因此证明∠CGE=∠ACB就是问题的关键，我们可通过证明三角形ABC和ECG全等来实现．
解答：证明：∵GC∥BH，DC∥AB，
∴∠HBA=∠GCD，
∴90°+∠HBA=∠GCD+90°，
∴∠GCE=∠ABC，
又∵AB=DC=EC，BC=CG，
∴△ABC≌△ECG（SAS），
∴∠CGE=∠ACB，
∵∠ACB+∠GCA=90°，
∴∠CGE+∠GCA=90°，
∴AC⊥EG．
∴∠HBA=∠GCD，
∴90°+∠HBA=∠GCD+90°，
∴∠GCE=∠ABC，
又∵AB=DC=EC，BC=CG，
∴△ABC≌△ECG（SAS），
∴∠CGE=∠ACB，
∵∠ACB+∠GCA=90°，
∴∠CGE+∠GCA=90°，
∴AC⊥EG．
点评：本题主要考查了正方形、平行四边形的性质，通过全等三角形来得出角相等是解题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
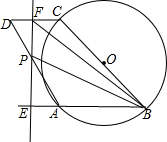如图，ABCD为平行四边形，以BC为直径的⊙O经过点A，∠D=60°，BC=2，一动点P在AD上移动，过点P作直线AB的垂线，分别交直线AB、CD于E、F，设点O到EF的距离为t，若B、P、F三点能构成三角形，设此时△BPF的面积为S．
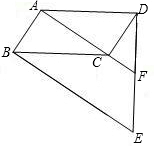如图，ABCD为平行四边形，BE∥AC，DE交AC延长线于F点，交BE于E点．
