题目内容
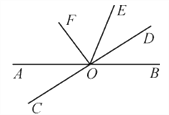
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.
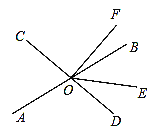
【答案】(1)72°(2)54°或126°
【解析】
(1)依据垂线的定义,即可得到∠DOE的度数,再根据角平分线的定义,即可得到∠BOD的度数,进而得出结论;
(2)分两种情况讨论,依据垂线的定义以及角平分线的定义,即可得到∠AOG的度数.
(1)∵OF⊥CD,∠EOF=54°,
∴∠DOE=90°﹣54°=36°,
又∵OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
∴∠AOC=72°;
(2)如图,若OG在∠AOD内部,则
由(1)可得,∠BOE=∠DOE=36°,
又∵∠GOE=90°,
∴∠AOG=180°﹣90°﹣36°=54°;
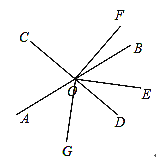
如图,若OG在∠COF内部,则
由(1)可得,∠BOE=∠DOE=36°,
∴∠AOE=180°﹣36°=144°,
又∵∠GOE=90°,
∴∠AOG=360°﹣90°﹣144°=126°.
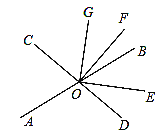
综上所述,∠AOG的度数为54°或126°.

练习册系列答案
相关题目