题目内容
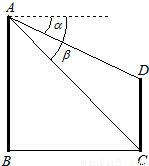
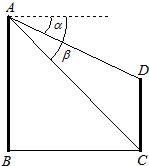如图，已知两座大楼的水平距离BC为100米，站在大楼AB楼顶A测得大楼CD楼顶D的俯角α为35°，楼底C的俯角β为43°，求两大楼的高度．（sin35°=0.574，cos35°=0.819，tan35°=0.700，sin43°=0.682，cos43°=0.731，tan43°=0.933）
分析：设AE=x，根据AE和α即可求得DE的长度，根据AE和β即可求得CE的长度，根据CD=CE-DE即可求得x的值，即可解题．
解答：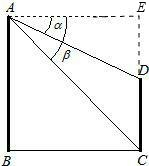
解：设AE=x，
在Rt△ADE中，DE=AE•tanα
在Rt△ACE中，CE=AE•tanβ
∵CD=CE-DE=100米，
即x（tanβ-tanα）=100，
解得x=
米=429.18米．
解：设AE=x，在Rt△ADE中，DE=AE•tanα
在Rt△ACE中，CE=AE•tanβ
∵CD=CE-DE=100米，
即x（tanβ-tanα）=100，
解得x=
| 100 |
| 0.233 |
点评：本题考查了三角形中三角函数的应用，本题中分别求CE、DE的长是解题的关键．
练习册系列答案
通城学典默写能手系列答案
相关题目
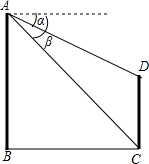如图，已知两座大楼的水平距离BC为100米，站在大楼AB楼顶A测得大楼CD楼顶D的俯角α为35°，楼底C的俯角β为43°，求两大楼的高度．（sin35°=0.574，cos35°=0.819，tan35°=0.700，sin43°=0.682，cos43°=0.731，tan43°=0.933）
（2012•安庆二模）如图是某小区的两座高楼，小明乘坐观光电梯在C处测得另一大楼顶部A的仰角为37°，电梯下降10m到D处时，又测得其底部B的俯角为48°．已知两座楼都为30层，每层高约2.8m，请帮小明求出两座高楼间的距离（参考数据：sin37°≈
如图，已知两座大楼的水平距离BC为100米，站在大楼AB楼顶A测得大楼CD楼顶D的俯角α为35°，楼底C的俯角β为43°，求两大楼的高度．（sin35°=0.574，cos35°=0.819，tan35°=0.700，sin43°=0.682，cos43°=0.731，tan43°=0.933）