题目内容
在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的测 量方案及数据如下:
量方案及数据如下:
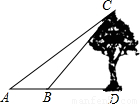
(1)在大树前选择一点A,测得点A看大树顶端C的仰角为30°;
(2)在点A和大树之间选择一点B(A、B、D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A、B间的距离为4米.请你根据以上数据求出大树CD的高度.
(精确到0.1,参考数据:
≈1.41
≈1.73)
 量方案及数据如下:
量方案及数据如下:(1)在大树前选择一点A,测得点A看大树顶端C的仰角为30°;
(2)在点A和大树之间选择一点B(A、B、D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A、B间的距离为4米.请你根据以上数据求出大树CD的高度.
(精确到0.1,参考数据:
| 2 |
| 3 |
分析:首先分析图形:本题涉及到两个直角三角形△DBC、△ADC,应利用其公共边CD构造等量关系,借助AB=AD-DB=4构造方程关系式,进而可求出答案.
解答: 解:设CD=x米,
解:设CD=x米,
在Rt△CBD中,tan45°=
∴BD=CD=x米
∴AD=AB+BD=(4+x)米
在Rt△ADC中
∵tan∠A=
∴tan30°=
即:
=
∴x≈5.4
∴CD的高度即树高约5.4米.
 解:设CD=x米,
解:设CD=x米,在Rt△CBD中,tan45°=
| CD |
| BD |
∴BD=CD=x米
∴AD=AB+BD=(4+x)米
在Rt△ADC中
∵tan∠A=
| CD |
| AD |
∴tan30°=
| x |
| 4+x |
即:
| x |
| 4+x |
| ||
| 3 |
∴x≈5.4
∴CD的高度即树高约5.4米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
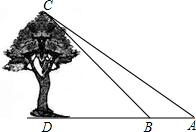 在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:
在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下: ,测得由点A看大树顶端
,测得由点A看大树顶端 的仰角为35°;在点
的仰角为35°;在点 (
( 在同一直线上),测得由点
在同一直线上),测得由点 的高度.(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70).
的高度.(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70).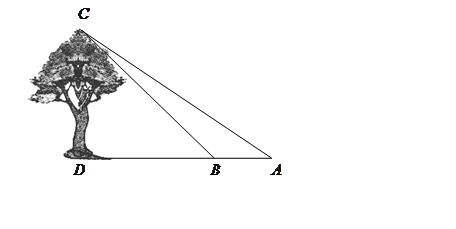

 ,测得由点
,测得由点 看大树顶端
看大树顶端 的仰角为35°;
的仰角为35°; (
( 在同一条直线上),测得由点
在同一条直线上),测得由点 .
. 的高度.(结果保留3个有效数字)
的高度.(结果保留3个有效数字) ≈1.41
≈1.41  ≈1.73)
≈1.73)