题目内容
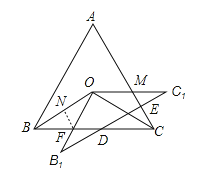
【题目】如图,点O是边长为![]() 的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1,B1C1交BC于点D,B1C1交AC于点E,则CE=( )
的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1,B1C1交BC于点D,B1C1交AC于点E,则CE=( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:令OB1与BC的交点为F,B1C1与AC的交点为M,过点F作FN⊥OB于点N,根据等边三角形的性质以及内心的性质找出△FOB为等腰三角形,求出BF的长,根据三角形内角和定理得出△FB1D是底角为30°的等腰三角形,得到FB1=FD,从而得到BD、CD的长,再根据三角形内角和定理得出∠DEC=90°,即可得出CE的长度.
详解:令OB1与BC的交点为F,B1C1与AC的交点为M,过点F作FN⊥OB于点N,如图所示.∵将△OBC绕点O逆时针旋转30°得到△OB1C1,∴∠BOF=30°.
∵点O是边长为4![]() 的等边△ABC的内心,∴∠OBF=30°,OB=
的等边△ABC的内心,∴∠OBF=30°,OB=![]() AB=4,∴△FOB为等腰三角形,BN=
AB=4,∴△FOB为等腰三角形,BN=![]() OB=2,∴BF=
OB=2,∴BF=![]() =
=![]() =OF.
=OF.
∵∠OBF=∠OB1D=∠BOB1=30°,∠BFO=∠B1FD,∴∠FDB1=30°,∴FB1=FD,∴BD=OB1=OB=4,∴DC=BC-BD=4![]() ﹣4.
﹣4.
∵∠FDB1=30°,∴∠EDC=30°.
∵∠BCA=60°,∴∠DEC=90°,∴EC=![]() DC=
DC=![]() .
.
故选C.

练习册系列答案
相关题目
【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
a | a+2 | a+4 | … |
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?