题目内容
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD. 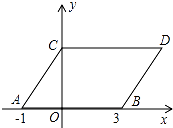
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
【答案】
(1)解:由平移可知:C(0,2),D(4,2)
(2)解:∵AB=4,CO=2,
∴S平行四边形ABOC=ABCO=4×2=8,
设M坐标为(0,m),
∴ ![]() ×4×|m|=8,解得m=±4
×4×|m|=8,解得m=±4
∴M点的坐标为(0,4)或(0,﹣4)
(3)解:①S梯形OCDB= ![]() ×(3+4)×2=7,
×(3+4)×2=7,
当点P运动到点B时,S△BOC最小,S△BOC的最小值= ![]() ×3×2=3,S△CDP+S△BOP<4,
×3×2=3,S△CDP+S△BOP<4,
当点P运动到点D时,S△BOC最大,S△BOC的最大值= ![]() ×4×2=4,S△CDP+S△BOP>3,
×4×2=4,S△CDP+S△BOP>3,
所以3<S△CDP+S△BOP<4;
②当点P在BD上,如图1,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠EPO﹣∠EPC=∠BOP﹣∠DCP,
∴∠BOP﹣∠DCP=∠CPO;
同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO
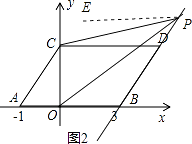
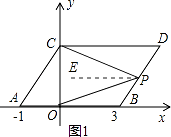
【解析】(1)根据点的平移规律易得点C,D的坐标;(2)先计算出S平行四边形ABOC=8,设M坐标为(0,m),根据三角形面积公式得 ![]() ×4×|m|=8,解得m=±4,于是可得M点的坐标为(0,4)或(0,﹣4);(3)①先计算出S梯形OCDB=7,再讨论:当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP<4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;②分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO﹣∠EPC=∠BOP﹣∠DCP,于是∠BOP﹣∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
×4×|m|=8,解得m=±4,于是可得M点的坐标为(0,4)或(0,﹣4);(3)①先计算出S梯形OCDB=7,再讨论:当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP<4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;②分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO﹣∠EPC=∠BOP﹣∠DCP,于是∠BOP﹣∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
【考点精析】关于本题考查的三角形的面积,需要了解三角形的面积=1/2×底×高才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案【题目】某单位欲招聘管理人员一名,对甲、乙、丙三人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,该单位组织200名职工利用投票推荐的方式对三人进行民主评议,三人的得票率(没有弃权票,每个职工只能推荐一个)如图所示,每得一票记1分,
(1)请计算出三人的民主评议得分;
(2)根据实际需要,该单位将笔试、面试、民主评议三项得分按4:3:3的比例确定每人的最后成绩,那么谁将被录用?请说明理由.

【题目】某小组7名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
劳动时间(小时) | 3 | 3.5 | 4 | 4.5 |
人 数 | 1 | 1 | 3 | 2 |
A. 中位数是4,众数是4B. 中位数是3.5,众数是4
C. 平均数是3.5,众数是4D. 平均数是4,众数是3.5

