Question

(本小题满分9分)

已知：△ABC是任意三角形．

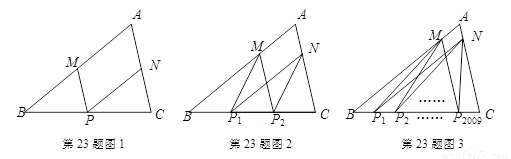
⑴如图1所示，点M、P、N分别是边AB、BC、CA的中点．求证：∠MPN=∠A．

⑵如图2所示，点M、N分别在边AB、AC上，且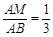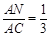，，点P1、P2是边BC的三等分点，你认为∠MP1N+∠MP2N=∠A是否正确？请说明你的理由．

⑶如图3所示，点M、N分别在边AB、AC上，且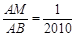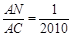，，点P1、P2、……、P2009是边BC的2010等分点，则∠MP1N+∠MP2N+……+∠MP2009N=____________．

（请直接将该小问的答案写在横线上．）

 

Answer 1

【答案】

 

（1）略

（2）正确

（3）∠A

【解析】⑴证明：∵点M、P、N分别是AB、BC、CA的中点，

         ∴线段MP、PN是△ABC的中位线，

∴MP∥AN，PN∥AM，  1分

         ∴四边形AMPN是平行四边形，    2分

         ∴∠MPN=∠A.       3分

⑵∠MP1N+∠MP2N=∠A正确.   4分

如图所示，连接MN，      5分

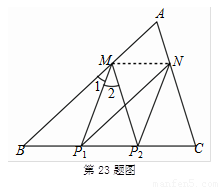
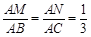∵，∠A=∠A，

∴△AMN∽△ABC，

∴∠AMN=∠B，，

∴MN∥BC，MN=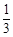BC，     6分

∵点P1、P2是边BC的三等分点，

∴MN与BP1平行且相等，MN与P1P2平行且相等，MN与P2C平行且相等，

∴四边形MBP1N、MP1P2N、MP2CN都是平行四边形，

∴MB∥NP1，MP1∥NP2，MP2∥AC，

    7分

∴∠MP1N=∠1，∠MP2N=∠2，∠BMP2=∠A，

∴∠MP1N+∠MP2N=∠1+∠2=∠BMP2=∠A.

    8分

⑶∠A.      9分