Question

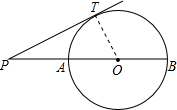
如图，PT切⊙O于点T，经过圆心O的割线PAB交⊙O于点A、B，已知PT=4，∠P=30°，则⊙O的直径AB等于______．

Answer 1

连接OT，由PT是⊙O的切线，得到∠PTO=90°，又∠P=30°，
∴OT=

1

2

PO，即OA=

1

2

OP，
∴PA=OA=OB，设PA=x，则PB=3x，
根据切割线定理得：PT²=PA•PB，即3x²=16，解得x=

4 3

3

，
则AB=2OA=

8 3

3

．
故答案为：

8 3

3

．