题目内容
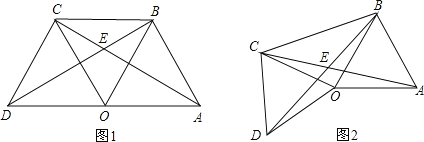
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
【答案】(1)60°;(2)60°
【解析】试题分析:(1),由△DOC和△ABO都是等边三角形,且点O是线段AD的中点,可得OD=OC=OB=OA,∠1=∠2=60°,∠4=∠5,从而利用外角的性质可得∠AEB=∠4+∠6=∠4+∠5=∠2=60°;
(2)由△DOC和△ABO都是等边三角形,且点O是线段AD的中点,可得OD=OC=OB=OA,∠1=∠2=60°,∠4=∠5,∠6=∠7,根据三角形内角和可得∠5=∠6,从而利用外角的性质可得∠AEB=∠2+∠6﹣∠5=∠2+∠5﹣∠5=∠2.
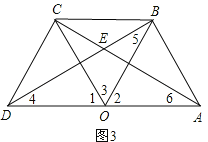
解:(1)如图3,
∵△DOC和△ABO都是等边三角形,
且点O是线段AD的中点,
∴OD=OC=OB=OA,∠1=∠2=60°,
∴∠4=∠5.
又∵∠4+∠5=∠2=60°,
∴∠4=30°.
同理∠6=30°.
∵∠AEB=∠4+∠6,
∴∠AEB=60°.
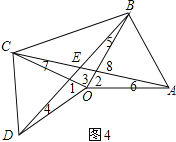
(2)如图4,
∵△DOC和△ABO都是等边三角形,
∴OD=OC,OB=OA,∠1=∠2=60°.
∴OD=OB,OA=OC,
∴∠4=∠5,∠6=∠7.
∵∠DOB=∠1+∠3,
∠AOC=∠2+∠3,
∴∠DOB=∠AOC.
∵∠4+∠5+∠DOB=180°,∠6+∠7+∠AOC=180°,
∴2∠5=2∠6,
∴∠5=∠6.
又∵∠AEB=∠8﹣∠5,∠8=∠2+∠6,
∴∠AEB=∠2+∠6﹣∠5=∠2+∠5﹣∠5=∠2,
∴∠AEB=60°.

 阅读快车系列答案
阅读快车系列答案