题目内容
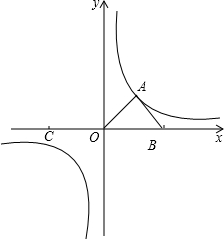
如图,点A在第一象限内,点B和点C在x轴上且关于原点对称,AO=AB,△ABO的面积为2且B(2,0)反比例函数过点A.(1)求反比例函数的关系式;
(2)如果P是这个反比例函数图象上一点,且∠BPC=90°,求点P的坐标.
分析:(1)若设y=
,因为AO=AB,△ABO的面积为2,所以k绝对值为2,根据图象位置可求k值;
(2)若设P(m,2m),则容易写出直线PB,PC解析式,从而求出m与系数关系,再根据系数之积为-1可求m值,既而写出P的坐标.
| k |
| x |
(2)若设P(m,2m),则容易写出直线PB,PC解析式,从而求出m与系数关系,再根据系数之积为-1可求m值,既而写出P的坐标.
解答:解:(1)设y=
,
∵AO=AB,△ABO的面积为2
∴K=2
∴y=
;
(2)设直线PB、PC解析式分别为y=k1x+b1、y=k2x+b2,点P(m,2m),B(2,0)代入其中:
得
,
,解得K1=
,K2=
∵∠BPC=90°
∴
×
=-1
∴m=
或m=-
∴点P坐标为(
,
)或(-
,-
).
| k |
| x |
∵AO=AB,△ABO的面积为2
∴K=2
∴y=
| 2 |
| x |
(2)设直线PB、PC解析式分别为y=k1x+b1、y=k2x+b2,点P(m,2m),B(2,0)代入其中:
得
|
|
| 2m |
| m-2 |
| 2m |
| m+2 |
∵∠BPC=90°
∴
| 2m |
| m-2 |
| 2m |
| m+2 |
∴m=
2
| ||
| 5 |
2
| ||
| 5 |
∴点P坐标为(
2
| ||
| 5 |
4
| ||
| 5 |
2
| ||
| 5 |
4
| ||
| 5 |
点评:此题难度中等,考查反比例函数、一次函数的图象和性质.同时同学们要掌握解方程组的方法.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
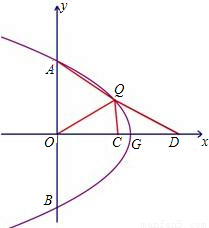
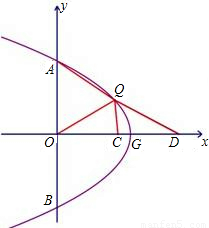
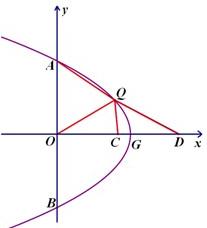 26、点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
26、点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.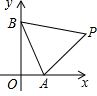 如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是
如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是