题目内容
(2011•玉溪一模)点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.(1)当m=2,点P横坐标为4时,求Q点的坐标;
(2)设点Q(a,b),用含m、b的代数式表示a;
(3)如图,点Q在第一象限内,点D在x轴的正半轴上,点C为OD的中点,QO平分∠AQC,AQ=2QC,当QD=m时,求m的值.
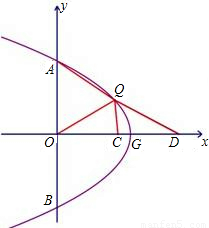
【答案】分析:(1)首先根据m的值确定出原抛物线的解析式,进而可求得P、G的坐标,过P作PE⊥x轴于E,过Q作QF⊥x轴于F,根据旋转的性质知:△GQF≌△PGE,则QF=GE、PE=GF,可据此求得点Q的坐标.
(2)已知了Q点坐标,即可得到QF、FG的长,仿照(1)的方法可求出点P的坐标,然后代入原抛物线的解析式中,可求得a、b、m的关系式.
(3)延长QC到E,使得QC=CE,那么AQ=QE;由于OD、QE互相平分,即四边形OEDQ是平行四边形(或证△QCD≌△ECO),那么QD=OE=m,而AQ=QE,且QO平分∠AQC,易证得△AQO≌△EQO,则OA=OE=m,即A点坐标为(0,m),然后将点A的坐标代入(2)的关系式中,即可求得m的值.
解答:解:(1)当m=2时,y=(x-2)2,
则G(2,0),
∵点P的横坐标为4,且P在抛物线上,
∴将x=4代入抛物线解析式得:y=(4-2)2=4,
∴P(4,4),(1分)
如图,连接QG、PG,过点Q作QF⊥x轴于F,过点P作PE⊥x轴于E,
依题意,可得△GQF≌△PGE;
则FQ=EG=2,FG=EP=4,
∴FO=2.
∴Q(-2,2).(2分)
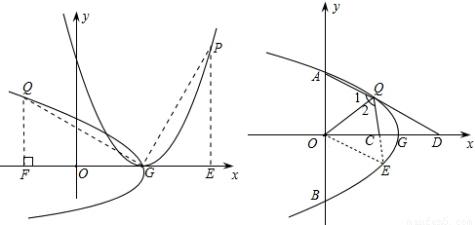
(2)已知Q(a,b),则GE=QF=b,FG=m-a;
由(1)知:PE=FG=m-a,GE=QF=b,即P(m+b,m-a),
代入原抛物线的解析式中,得:m-a=(m+b)2-2m(m+b)+m2
m-a=m2+b2+2mb-2m2-2mb+m2
a=m-b2,
故用含m,b的代数式表示a:a=m-b2.(4分)
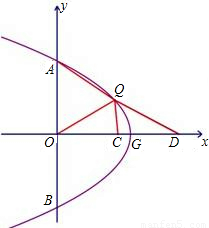
(3)如图,延长QC到点E,使CE=CQ,连接OE;
∵C为OD中点,
∴OC=CD,
∵∠ECO=∠QCD,
∴△ECO≌△QCD,
∴OE=DQ=m;(5分)
∵AQ=2QC,
∴AQ=QE,
∵QO平分∠AQC,
∴∠1=∠2,
∴△AQO≌△EQO,(6分)
∴AO=EO=m,
∴A(0,m),(7分)
∵A(0,m)在新的函数图象上,
∴0=m-m2
∴m1=1,m2=0(舍),
∴m=1.(8分)
点评:此题主要考查了图形的旋转变换、全等三角形的判定和性质、函数图象上点的坐标意义等知识,难度较大.
(2)已知了Q点坐标,即可得到QF、FG的长,仿照(1)的方法可求出点P的坐标,然后代入原抛物线的解析式中,可求得a、b、m的关系式.
(3)延长QC到E,使得QC=CE,那么AQ=QE;由于OD、QE互相平分,即四边形OEDQ是平行四边形(或证△QCD≌△ECO),那么QD=OE=m,而AQ=QE,且QO平分∠AQC,易证得△AQO≌△EQO,则OA=OE=m,即A点坐标为(0,m),然后将点A的坐标代入(2)的关系式中,即可求得m的值.
解答:解:(1)当m=2时,y=(x-2)2,
则G(2,0),
∵点P的横坐标为4,且P在抛物线上,
∴将x=4代入抛物线解析式得:y=(4-2)2=4,
∴P(4,4),(1分)
如图,连接QG、PG,过点Q作QF⊥x轴于F,过点P作PE⊥x轴于E,
依题意,可得△GQF≌△PGE;
则FQ=EG=2,FG=EP=4,
∴FO=2.
∴Q(-2,2).(2分)

(2)已知Q(a,b),则GE=QF=b,FG=m-a;
由(1)知:PE=FG=m-a,GE=QF=b,即P(m+b,m-a),
代入原抛物线的解析式中,得:m-a=(m+b)2-2m(m+b)+m2
m-a=m2+b2+2mb-2m2-2mb+m2
a=m-b2,
故用含m,b的代数式表示a:a=m-b2.(4分)
(3)如图,延长QC到点E,使CE=CQ,连接OE;
∵C为OD中点,
∴OC=CD,
∵∠ECO=∠QCD,
∴△ECO≌△QCD,
∴OE=DQ=m;(5分)
∵AQ=2QC,
∴AQ=QE,
∵QO平分∠AQC,
∴∠1=∠2,
∴△AQO≌△EQO,(6分)
∴AO=EO=m,
∴A(0,m),(7分)
∵A(0,m)在新的函数图象上,
∴0=m-m2
∴m1=1,m2=0(舍),
∴m=1.(8分)
点评:此题主要考查了图形的旋转变换、全等三角形的判定和性质、函数图象上点的坐标意义等知识,难度较大.

练习册系列答案
相关题目

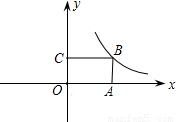
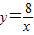 的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.
的图象过矩形OABC的顶点B,OA、0C分别在x轴、y轴的正半轴上,OA:0C=2:1.