��Ŀ����
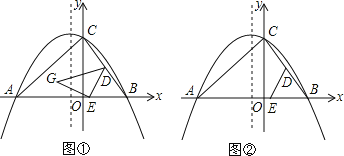
����Ŀ����֪����ABC��ƽ��ֱ������ϵ�е�λ����ͼ����ʾ��A������Ϊ����6��0����B������Ϊ��4��0������DΪBC���е㣬��EΪ�߶�AB��һ���㣬����DE������A��B��C����������ߵĽ���ʽΪy��ax2+bx+8��
��1���������ߵĽ���ʽ��
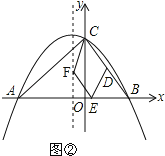
��2����ͼ�٣�����BDE��DEΪ�ᷭ�ۣ���B�ĶԳƵ�Ϊ��G������Gǡ�����������ߵĶԳ�����ʱ����G������ꣻ
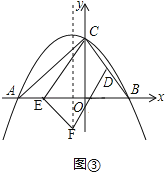
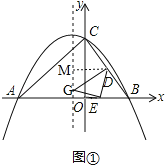
��3����ͼ�ڣ�����E���߶�AB���˶�ʱ��������y��ax2+bx+8�ĶԳ������Ƿ���ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��G�������Ϊ����1��4+
����2��G�����������1��4+![]() ����1��4��
����1��4��![]() ������3�����ڣ���F�������ǣ���1��4��������1����4����1��12����
������3�����ڣ���F�������ǣ���1��4��������1����4����1��12����
��������
��1������������y��ax2+bx+8������A����6��0����B��4��0����Ӧ�ô���ϵ��������������ߵĽ���ʽ���ɣ�
��2��������DM�������ߵĶԳ����ڵ�M����G�������Ϊ����1��n�������ݷ��۵����ʣ��ɵ�BD��DG��Ȼ��ֱ������D����M��������Ƕ��٣��Լ�BC��BD��ֵ���Ƕ��٣������Rt��GDM�У����ݹ��ɶ��������n��ֵ���������G������꣮
��3���������⣬������������ٵ�CD��EF���ҵ�E��x���������ʱ���ڵ�CD��EF���ҵ�E��x��ĸ�����ʱ���۵�CE��DFʱ��Ȼ�����ƽ���ı��ε����ʣ������F��������Ƕ��ټ��ɣ�
�⣺��1����������y��ax2+bx+8������A����6��0����B��4��0����
��![]()
���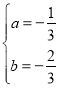
�������ߵĽ���ʽ�ǣ�![]()
��2����ͼ�٣���DM�������ߵĶԳ����ڵ�M����
��G�����������1��n����
�ɷ��۵����ʣ��ɵ�BD��DG��
��B��4��0����C��0��8������DΪBC���е㣬
���D�������ǣ�2��4����
���M�������ǣ���1��4����DM��2������1����3��
��B��4��0����C��0��8����
��BC��![]() ��4
��4![]() ��
��
��BD=2![]() ��
��
��Rt��GDM��
32+��4��n��2��20��
���n��4��![]() ��
��
��G�����������1��4+![]() ����1��4��
����1��4��![]() ����
����
��3��������y��ax2+bx+8�ĶԳ����ϴ��ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ�
�ٵ�CD��EF���ҵ�E��x���������ʱ����ͼ�ڣ�
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ���1��d����
��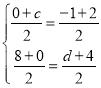
���![]()
���F�������ǣ���1��4������E�������ǣ�1��0����
�ڵ�CD��EF���ҵ�E��x��ĸ�����ʱ����ͼ�ۣ�
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ���1��d����
��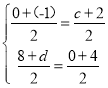
���![]()
���F�������ǣ���1����4������E�������ǣ���3��0����
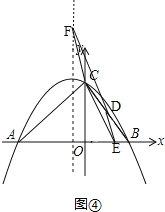
�۵�CE��DFʱ����ͼ�ܣ���
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ���1��d����
��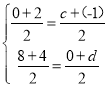
���![]()
���F�������ǣ���1��12������E�������ǣ�3��0����
���ϣ��ɵ�
������y��ax2+bx+8�ĶԳ����ϴ��ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ�
��F�������ǣ���1��4��������1����4����1��12����

����Ŀ������������һ���ߵı߳�Ϊ3�������������ߵı߳��ǹ���x��һԪ���η���x2��12x+k=0������������k��ֵ��________��
����Ŀ��Ϊ���˽�ijС�������������������ɨ��֧�������������������������������Ĵ�����ϲ���̶ȣ���������С��һ�������꣨ÿ������ֻ��ѡһ�����������������Ƴ���ͼ��ʾͳ�Ʊ�������ͳ��ͼ.
������ϲ�������Ĵ�������ͳ�Ʊ�
��Ŀ | ���������� | �ٷֱ� |
�������� | 5 |
|
ɨ��֧�� | 15 |
|
���� |
|
|
���� | 10 |
|
������ϲ�������Ĵ�����������ͳ��ͼ
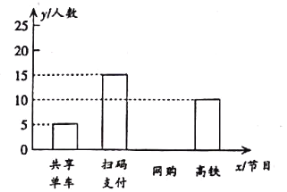
��1������![]() ��ֵ
��ֵ![]() ��
��
��2���벹ȫ����ͳ��ͼ��
��3���ڱ�����ϲ�������������������У�С��һ����ʹ�ù��������Ĵ����ֱ�Ϊ��1��3��5��12��![]() ��������
��������![]() ���������ݵ���λ����ֱ��д���������ݵ�ƽ����.
���������ݵ���λ����ֱ��д���������ݵ�ƽ����.
����Ŀ���ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ����������������Ϣ���±���
ʱ��x���죩 | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x��40 | 90 |
ÿ������������ | 200��2x | |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ[
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�����.