题目内容
已知:如图,△ABE中,AB=AE,以AB为直径的⊙O交BE于C,过点C作CD⊥AE于D,DC的延长线 与AB的延长线交于点P.
与AB的延长线交于点P.(1)求证:PD是⊙O的切线;
(2)若AE=10,BE=12,求DC的长.
分析:(1)连接OC,PD⊥AE,则∠DCE+∠E=90°,由AB=AE,OB=OC,得∠CBA=∠E=∠BCO,得出∠PCB+∠BCO=90°,即可得出PD是⊙O的切线.
(2)连接AC,由勾股定理得AC=8,即可证明△EDC∽△BCA,则
=
,代入数据即可得出答案.
(2)连接AC,由勾股定理得AC=8,即可证明△EDC∽△BCA,则
| DC |
| CA |
| EC |
| BA |
解答: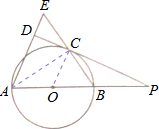 (1)证明:连接OC,
(1)证明:连接OC,
∵PD⊥AE于D,
∴∠DCE+∠E=90°,
∵AB=AE,OB=OC,
∴∠CBA=∠E=∠BCO,
∵∠DCE=∠PCB,
∴∠PCB+∠BCO=90°,
∴PD是⊙O的切线.
(2)解:连接AC,∵AB=AE=10,AB是⊙O的直径,BE=12,
∴AC=BE,EC=BC=6,在△ABC中,AB=10,BC=6,∠ACB=90°,由勾股定理得AC=8.
又∵∠CBA=∠E,∠EDC=∠ACB=90°,
∴△EDC∽△BCA,
∴
=
,
∴
=
,
∴DC=
…5分
 (1)证明:连接OC,
(1)证明:连接OC,∵PD⊥AE于D,
∴∠DCE+∠E=90°,
∵AB=AE,OB=OC,
∴∠CBA=∠E=∠BCO,
∵∠DCE=∠PCB,
∴∠PCB+∠BCO=90°,
∴PD是⊙O的切线.
(2)解:连接AC,∵AB=AE=10,AB是⊙O的直径,BE=12,
∴AC=BE,EC=BC=6,在△ABC中,AB=10,BC=6,∠ACB=90°,由勾股定理得AC=8.
又∵∠CBA=∠E,∠EDC=∠ACB=90°,
∴△EDC∽△BCA,
∴
| DC |
| CA |
| EC |
| BA |
∴
| DC |
| 8 |
| 6 |
| 10 |
∴DC=
| 24 |
| 5 |
点评:本题考查了相似三角形的判定和性质、勾股定理、切线的判定和性质,是重点内容要熟练掌握.

练习册系列答案
相关题目
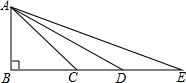 已知:如图,∠ABE=90°,且AB=BC=CD=DE,请认真研究图形与所给条件,然后回答:图中是否存在相似的三角形?若存在,请加以说明;若不存在,请说明理由.
已知:如图,∠ABE=90°,且AB=BC=CD=DE,请认真研究图形与所给条件,然后回答:图中是否存在相似的三角形?若存在,请加以说明;若不存在,请说明理由.
