题目内容
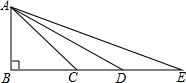已知：如图，∠ABE=90°，且AB=BC=CD=DE，请认真研究图形与所给条件，然后回答：图中是否存在相似的三角形？若存在，请加以说明；若不存在，请说明理由．
分析：分别根据勾股定理求各三角形的边长，求各边长的比值，根据各边长的比值相等可以判定相似三角形，即可解题．
解答：解：存在，△ACD∽△ECA．
设AB=a，则CD=a，CE=2a，AC=
a．
∴
=
，
=
，
∴
=
．
又∵∠ACD=∠ECA，
∴△ACD∽△ECA．
设AB=a，则CD=a，CE=2a，AC=
| 2 |
∴
| AC |
| EC |
| ||
| 2 |
| CD |
| CA |
| ||
| 2 |
∴
| AC |
| CE |
| CD |
| AC |
又∵∠ACD=∠ECA，
∴△ACD∽△ECA．
点评：本题考查了相似三角形对应边比值相等的性质，勾股定理在直角三角形中的运用，本题中计算各边长的值是解题的关键．
练习册系列答案
相关题目
与AB的延长线交于点P．
