题目内容
 如图,△ABC的角平分线AD的延长线交△ABC的外接圆于点E.下列四个结论:
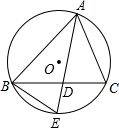
如图,△ABC的角平分线AD的延长线交△ABC的外接圆于点E.下列四个结论:
①∠BAE=∠DBE;②△BAE∽△DBE;③△DBE∽△DAC;④DB:BA=DC:CA,其中正确的个数是
- A.1
- B.2
- C.3
- D.4
D
分析:利用角平分线的定义得到两个圆周角相等,然后得到相等的弧,利用同弧所对的圆周角相等即可得到相等的圆周角,然后可以证明相似三角形并根据相似三角形得到对应边成比例.
解答:∵△ABC的角平分线AD的延长线交△ABC的外接圆于点E,
∴弧BE=弧CE,
∴∠BAE=∠DBE,
故①正确;
∵∠BAE=∠DBE,∠E=∠E,
∴△BAE∽△DBE,
故②正确;
∵∠EBC=∠EAC,∠E=∠C,
∴△DBE∽△DAC,
故③正确;
∵△BAE∽△DBE,
∴DB:BA=DE:BE;
∵△DBE∽△DAC,
∴DE:BE=DC:BA,
∴DB:BA=DC:CA,
故④正确;
故选D.
点评:本题考查了圆周角定理及相似三角形的判断与性质,题目中涉及的知识点比较多,但相对比较简单.
分析:利用角平分线的定义得到两个圆周角相等,然后得到相等的弧,利用同弧所对的圆周角相等即可得到相等的圆周角,然后可以证明相似三角形并根据相似三角形得到对应边成比例.
解答:∵△ABC的角平分线AD的延长线交△ABC的外接圆于点E,
∴弧BE=弧CE,
∴∠BAE=∠DBE,
故①正确;
∵∠BAE=∠DBE,∠E=∠E,
∴△BAE∽△DBE,
故②正确;
∵∠EBC=∠EAC,∠E=∠C,
∴△DBE∽△DAC,
故③正确;
∵△BAE∽△DBE,
∴DB:BA=DE:BE;
∵△DBE∽△DAC,
∴DE:BE=DC:BA,
∴DB:BA=DC:CA,
故④正确;
故选D.
点评:本题考查了圆周角定理及相似三角形的判断与性质,题目中涉及的知识点比较多,但相对比较简单.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
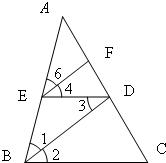 23、如图,BD是∠ABC的平分线,ED∥BC,∠4=∠3,则EF也是∠AED的平分线.
23、如图,BD是∠ABC的平分线,ED∥BC,∠4=∠3,则EF也是∠AED的平分线.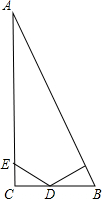 如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.
如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.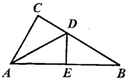 16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是
16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是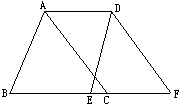
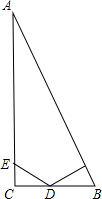 如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.
如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.