题目内容
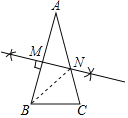
【题目】已知,如图,△ABC中,AB=AC,∠A=36°.
(1)作AB边的垂直平分线,垂足为M,交AC于N,连结BN.(不写作法,保留作图痕迹)
(2)①直接写出∠ABN的度数为 ;
②若BC=12,直接写出BN的长为 .

【答案】(1)详见解析;(2)36°,12.
【解析】
(1)根据题意,根据垂直平分线的画法进行尺规作图即可;
(2)根据垂直平分线上的点到线段两端的距离相等即可得出∠ABN=∠A;
(3)根据垂直平分线的性质和三角形外角定理,可知∠BNC=72°,再根据AB=AC,∠A=36°,得出∠C=72°,可得BC=BN=12.
解:(1)如图所示:MN即为所求;
(2)①∠ABN的度数为:36°;
②∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵直线MN垂直平分线AB,
∴AN=BN,
∴∠ABN=∠A=36°,
∴∠CBN=36°,
∴∠BNC=72°,
∴BC=BN=12.
故答案为:36°,12.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
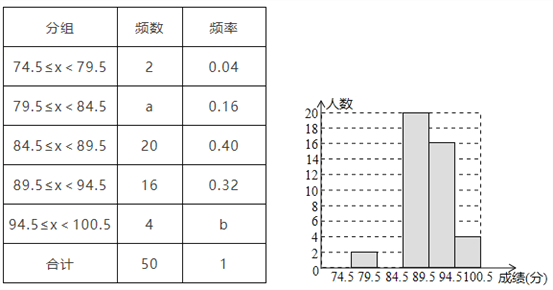
【题目】我市某小区开展了“节约用水为环保做贡献”的活动,为了解居民用水情况,在小区随机抽查了10户家庭的月用水量,结果如下表
月用水量(吨) | 8 | 9 | 10 |
户数 | 2 | 6 | 2 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A. 方差是4 B. 极差2 C. 平均数是9 D. 众数是9