题目内容
1、求证:
(1)8|(551999+17);
(2) 8(32n+7);
(3)17|(191000-1).
(1)8|(551999+17);
(2) 8(32n+7);
(3)17|(191000-1).
分析:(1)根据55+1能被8整除可得出551999+1也能被8整除,进而可得出答案;
(2)先根据32-1=9-1=8能被8整除可得出32n-1能被8整除,故32n-1+8能被8整除,即32n+7能被8整除;
(3)根据19-2=17能被17整除,可知194-(24+1)能被17整除,进而可得出(194)250+1250-2能被17整除,故可得出结论.
(2)先根据32-1=9-1=8能被8整除可得出32n-1能被8整除,故32n-1+8能被8整除,即32n+7能被8整除;
(3)根据19-2=17能被17整除,可知194-(24+1)能被17整除,进而可得出(194)250+1250-2能被17整除,故可得出结论.
解答:证明:(1)∵55+1能被8整除,
∴551999+1也能被8整除,
∵16能被8整除,
∴551999+1+16=551999+17能被8整除;
(2)∵32-1=9-1=8能被8整除,
∴32n-1能被8整除,
∴32n-1+8能被8整除,
即32n+7能被8整除;
(3)∵19-2=17能被17整除,
∴194-(24+1)能被17整除,
∵191000=(194)250+1250-2能被17整除,
∴17|(191000-1).
∴551999+1也能被8整除,
∵16能被8整除,
∴551999+1+16=551999+17能被8整除;
(2)∵32-1=9-1=8能被8整除,
∴32n-1能被8整除,
∴32n-1+8能被8整除,
即32n+7能被8整除;
(3)∵19-2=17能被17整除,
∴194-(24+1)能被17整除,
∵191000=(194)250+1250-2能被17整除,
∴17|(191000-1).
点评:本题考查的是同余问题,熟知同余问题的等价关系式解答此题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
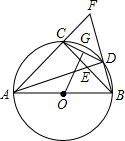 如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD与⊙O交于点D,与BC交于点E,延长BD,与AC的延长线交于点F,连接CD,G是CD的中点,连接OG.
如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD与⊙O交于点D,与BC交于点E,延长BD,与AC的延长线交于点F,连接CD,G是CD的中点,连接OG. 24、如图,BD是?ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.
24、如图,BD是?ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.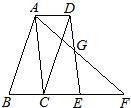 27、在平行四边形ABCD中,BC=CE,AC=CF,AF、DE交于点G,B、C、E、F在一直线上.
27、在平行四边形ABCD中,BC=CE,AC=CF,AF、DE交于点G,B、C、E、F在一直线上. 20、已知,如图,C为线段AB的中点,CD平分∠ACE,CE平分∠BCD,且CD=CE,求证:AD=BE.
20、已知,如图,C为线段AB的中点,CD平分∠ACE,CE平分∠BCD,且CD=CE,求证:AD=BE.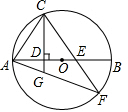 DB上任意一点(点D、B除外),直线CE交⊙O于点F,连接AF与直线CD交于点G.
DB上任意一点(点D、B除外),直线CE交⊙O于点F,连接AF与直线CD交于点G.