题目内容
在平面直角坐标系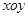 中,已知点
中,已知点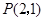 ,点
,点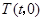 是
是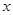 轴上的一个动点,当
轴上的一个动点,当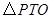 是等腰三角形时,
是等腰三角形时,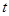 值的个数是 .
值的个数是 .
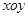 中,已知点
中,已知点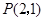 ,点
,点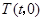 是
是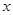 轴上的一个动点,当
轴上的一个动点,当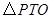 是等腰三角形时,
是等腰三角形时,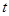 值的个数是 .
值的个数是 .4个
分类讨论①OP作腰,O是顶点,即以O为圆心,OP长为半径画弧,与x轴的交点即是所求;②OP是底边,所构成的等腰三角形与x轴交点是(x,0),然后利用OT=PT,结合两点之间的距离公式,可得寡欲x的方程,解即可;③△POT是以AP为底边上的垂直平分线的等腰三角形,易求T的坐标.
解:如右图所示,
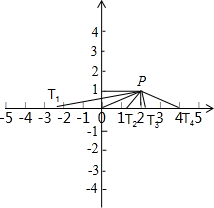
①∵P点的坐标是(2,1),
∴OP=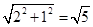 ,
,
∴以O为圆心,OP长为半径画弧(OP做腰),
交x轴分别是( ,0),(-
,0),(- ,0);
,0);
②设T的坐标是(x,0),OP做等腰三角形的底边,那么有
即x2=4-4x+x2+1,
解得x=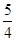 ,
,
故T的坐标是(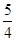 ,0);
,0);
③AP是等腰三角形底边的垂直平分线,那么O点的对称点坐标是(4,0).
故t的值有4个.
解:如右图所示,

①∵P点的坐标是(2,1),
∴OP=
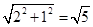 ,
,∴以O为圆心,OP长为半径画弧(OP做腰),
交x轴分别是(
 ,0),(-
,0),(- ,0);
,0);②设T的坐标是(x,0),OP做等腰三角形的底边,那么有

即x2=4-4x+x2+1,
解得x=
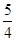 ,
,故T的坐标是(
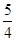 ,0);
,0);③AP是等腰三角形底边的垂直平分线,那么O点的对称点坐标是(4,0).
故t的值有4个.

练习册系列答案
相关题目
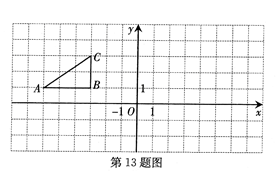
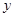 轴上确定点P,使△AOP为等腰三角形,则符合条件的有_______个.
轴上确定点P,使△AOP为等腰三角形,则符合条件的有_______个.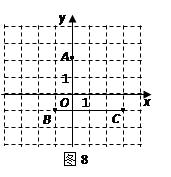
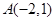 关于
关于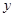 轴的对称点
轴的对称点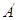 的坐标是 ▲ .
的坐标是 ▲ .