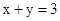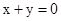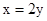题目内容
某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?
(1)根据题意,甲和乙两同学分别列出的方程组如下:
甲: 乙:
乙:
根据两位同学所列的方程组,请你分别指出未知数x,y表示的意义:
甲:x表示_________,y表示_________;
乙:x表示_________,y表示_________;
(2)求出做成的A型盒子和B型盒子分别有多少个(写出完整的解答过程)?

(1)根据题意,甲和乙两同学分别列出的方程组如下:
甲:
 乙:
乙:
根据两位同学所列的方程组,请你分别指出未知数x,y表示的意义:
甲:x表示_________,y表示_________;
乙:x表示_________,y表示_________;
(2)求出做成的A型盒子和B型盒子分别有多少个(写出完整的解答过程)?

(1)A型盒子的个数;B型盒子的个数 做A型盒子的正方形纸板数;做B型盒子的正方形纸板
(2)A型盒子60个,B型盒子40个
试题分析:本题考查了由实际问题抽象二元一次方程组的知识,
(1)注意仔细观察A、B型号长方体的特点,由长方形纸板、正方形纸板的数量建立方程组.从两个方向考虑:一种方案定盒子数,甲方案:x表示:A型盒子的个数,y表示:B型盒子的个数 ;另一种方案定纸板数,乙方案:x表示:做A型盒子的正方形纸板数,y表示:做B型盒子的正方形纸板 ;
(2)根据前面方案,通过确定盒子数或纸板数,都可解决问题。如设做A型盒子用了正方形纸板x张,做B型盒子用了正方形纸板y张,则可得A型盒子x个,B型盒子
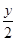 个,根据长方形纸板360张,正方形纸板140张,可得出方程组.
个,根据长方形纸板360张,正方形纸板140张,可得出方程组.试题解析:
(1)x,y表示的意义:
甲:x表示:A型盒子的个数,y表示:B型盒子的个数
乙:x表示:做A型盒子的正方形纸板数,
y表示:做B型盒子的正方形纸板
(2)解:设做成的A型盒子x个,做成的B型盒子y个
甲:
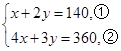
①×4-②得5y="200"
有y=40
代入①得x=60
答:做成的A型盒子和B型盒子分别有60个和40个
乙:①x+y=140,②4x+(3/2)y=360
①×4-②得5y/2=200
有y=80
代入①得x=60
可做成的A型盒子60个,可做成的B型盒子40个。

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
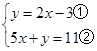 .
.
 的解是 .
的解是 . 的解也是二元一次方程2x+3y=6的解,则k的值是( )
的解也是二元一次方程2x+3y=6的解,则k的值是( )

 ,则这个方程可能是( )
,则这个方程可能是( )