题目内容
（2008•呼和浩特）将图中的矩形ABCD沿对角线AC剪开，再把△ABC沿着AD方向平移，得到图2中的△A′B′C′，其中E是A′B′与AC的交点，F是A′C′与CD的交点．在图中除△ADC与△C′B′A′全等外，还有几对全等三角形（不添加辅助线和字母）请一一指出，并选择其中一对证明．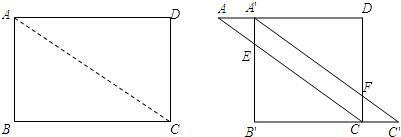
分析：本题是开放题，应先确定选择哪对三角形，再对应三角形全等条件求解．三角形全等条件中必须是三个元素，并且一定有一组对应边相等．
解答：解：（1）△AA'E≌△C'CF
（2）△A'DF≌△CB'E
证明：（1）∵四边形ABCD是矩形
∴AD∥BC
∴∠DAC=∠ACB
由平移的性质得：∠ACB=∠C'，AA'=CC'，∠AA'E=∠C'CF=90°
∴∠DAC=∠C′
∴△AA'E≌△C'CF
（2）∵四边形ABCD是矩形
∴AD=B'C'，且∠DAC=∠ACB
由平移的性质得：AA'=CC'，∠D=∠B'=90°，∠ACB=∠C'
∴A'D=B'C
又∠DA'F=∠C'，∠ECB'=∠DAC
∴∠DA'F=∠ECB'
∴△A'DF≌△CB'E
（2）△A'DF≌△CB'E
证明：（1）∵四边形ABCD是矩形
∴AD∥BC
∴∠DAC=∠ACB
由平移的性质得：∠ACB=∠C'，AA'=CC'，∠AA'E=∠C'CF=90°
∴∠DAC=∠C′
∴△AA'E≌△C'CF
（2）∵四边形ABCD是矩形
∴AD=B'C'，且∠DAC=∠ACB
由平移的性质得：AA'=CC'，∠D=∠B'=90°，∠ACB=∠C'
∴A'D=B'C
又∠DA'F=∠C'，∠ECB'=∠DAC
∴∠DA'F=∠ECB'
∴△A'DF≌△CB'E
点评：本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等．
练习册系列答案
相关题目
，
），B点在y轴上，直线与x轴的交点为F，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于E点．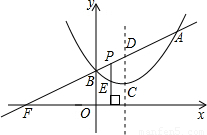
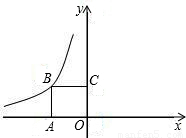
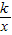（k＜0，x＜0）的图象上，点P（m，n）是函数y=
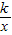（k＜0，x＜0）的图象上异于B的任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E，F．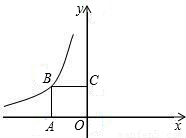
，
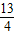），B点在y轴上，直线与x轴的交点为F，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于E点．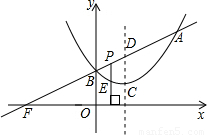
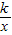（k＜0，x＜0）的图象上，点P（m，n）是函数y=
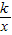（k＜0，x＜0）的图象上异于B的任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E，F．