题目内容
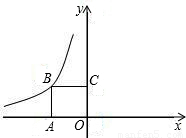
（2008•呼和浩特）如图，正方形OABC的面积为4，点O为坐标原点，点B在函数y=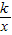
（k＜0，x＜0）的图象上，点P（m，n）是函数y=
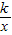（k＜0，x＜0）的图象上异于B的任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E，F．（1）设矩形OEPF的面积为S1，试判断S1是否与点P的位置有关；（不必说明理由）
（2）从矩形OEPF的面积中减去其与正方形OABC重合的面积，剩余面积记为S2，写出S2与m的函数关系，并标明m的取值范围．
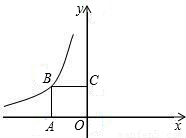
【答案】分析：（1）点P是函数y=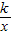
的图象上一点，因此矩形OEPF面积一定是4，所以S1与点P的位置无关；
（2）观察图形，S2为两矩形面积之差，根据坐标意义，可用m代数式表示它们面积，即解．
解答：解：（1）S1与点P的位置无关；
（2）∵正方形OABC的面积为4，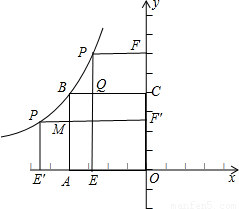
∴OC=OA=2．
∴B（-2，2）．
把B（-2，2）代入y=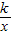
中，2=
；
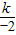∴k=-4．
∴解析式为y=-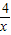
．
∵P（m，n）在y=-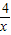
的图象上，
∴
．
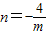①当P在B点上方时，
S2=S矩形PEOF-S四边形EOCQ，
-
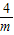（-m）-2（-m）
=4+2m（-2＜m＜0）；
②当P在B点下方时，
S2=S矩形PE′OF′-S矩形MAOF′=-m×（-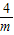
）-2×（-
，
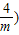=4+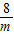
（m＜-2）．
综上所述S2=
．
点评：本题考查了反比例函数与正方形性质的综合应用，综合性较强，同学们要重点掌握．
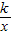的图象上一点，因此矩形OEPF面积一定是4，所以S1与点P的位置无关；（2）观察图形，S2为两矩形面积之差，根据坐标意义，可用m代数式表示它们面积，即解．
解答：解：（1）S1与点P的位置无关；
（2）∵正方形OABC的面积为4，
∴OC=OA=2．
∴B（-2，2）．
把B（-2，2）代入y=
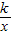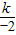中，2=；∴k=-4．
∴解析式为y=-
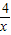．∵P（m，n）在y=-
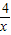的图象上，∴
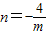．①当P在B点上方时，
S2=S矩形PEOF-S四边形EOCQ，
-
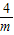（-m）-2（-m）=4+2m（-2＜m＜0）；
②当P在B点下方时，
S2=S矩形PE′OF′-S矩形MAOF′=-m×（-
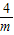）-2×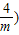（-，=4+
（m＜-2）．综上所述S2=
．点评：本题考查了反比例函数与正方形性质的综合应用，综合性较强，同学们要重点掌握．
练习册系列答案
应用题作业本系列答案
相关题目
，
），B点在y轴上，直线与x轴的交点为F，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于E点．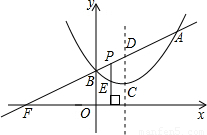
，
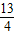），B点在y轴上，直线与x轴的交点为F，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于E点．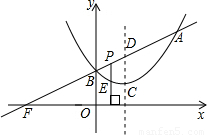
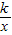（k＜0，x＜0）的图象上，点P（m，n）是函数y=
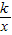（k＜0，x＜0）的图象上异于B的任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E，F．