题目内容
把长为8cm的矩形按虚线对折，按图中的虚线剪出一个直角梯形，打开得到一个等腰梯形，剪掉部分的面积为6cm2，则打开后梯形的周长是 ▲ .
分析：根据剪去的三角形的面积可得矩形的宽，利用勾股定理即可求得等腰梯形的腰长，根据折叠可得梯形其余边长，相加即为梯形的周长．
解答：解：∵剪掉部分的面积为6cm2，
∴矩形的宽为2，
易得梯形的下底为矩形的长，上底为（8÷2-3）×2=2，腰长为
=
，
∴打开后梯形的周长是（10+2）cm．
故答案为：10+2．
解答：解：∵剪掉部分的面积为6cm2，
∴矩形的宽为2，
易得梯形的下底为矩形的长，上底为（8÷2-3）×2=2，腰长为
=，∴打开后梯形的周长是（10+2
）cm．故答案为：10+2
．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
，则
（ ）
中，点D、E、F分别在边
、
、
上，且
，
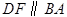．下列四种说法： ①四边形
是平行四边形；②如果
，那么四边形
平分
，那么四边形
且
，那么四边形
