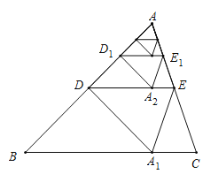
题目内容
【题目】在一次购物中,小悦和小惠都准备从“微信”“支付宝”“银行卡”“现金”四种支付方式中任选一种进行支付.
(1)小悦用“微信”支付是__________事件(填“不可能”或“必然”或“随机”),小惠用“微信”支付的概率是__________.
(2)请用画树状图或列表的方法求出两人恰好选择同一种支付方式的概率.
【答案】(1)随机,![]() ;(2)列表见解析,
;(2)列表见解析,![]()
【解析】
(1)根据小悦用“微信”支付可能发生也可能不发生即可判断,总共有4中支付方法,而“微信”支付是其中的一种,由此可求出小惠用“微信”支付的概率;
(2)用树状图或列表法表示出所有的情况数,从中找出两人恰好选择同一种支付方式的情况数,利用所求情况数与总数之比求概率即可.
解:(1) 小悦用“微信”支付可能发生也可能不发生,所以是随机事件;
总共有4中支付方法,而“微信”支付是其中的一种,所以小惠用“微信”支付的概率为![]() ;
;
(2) “微信”“支付宝”“银行卡”“现金”四种支付方式分别用字母A,B,C,D代替,列表如下:
小惠选择的支付方式 小悦选择的支付方式 | A | B | C | D |
A | (A,A) | (A,B) | (A,C) | (A,D) |
B | (B,A) | (B,B) | (B,C) | (B,D) |
C | (C,A) | (C,B) | (C,C) | (C,D) |
D | (D,A) | (D,B) | (D,C) | (D,D) |
由表可知,共有16种结果,且每种结果出现的可能性相同,其中两人恰好选择同一种支付方式的有4种,故P(两人恰好选择同一种支付方式)= ![]() .
.

【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?