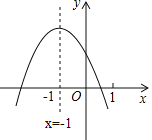题目内容
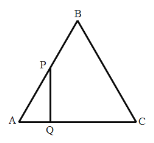
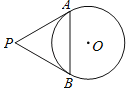
【题目】如图，已知PA，PB分别切⊙O于点A、B，∠P＝60°，PA＝8，那么弦AB的长是_____；连接OA、OB，则∠AOB＝_____．
【答案】8 120°
【解析】
由切线长定理可得PA=PB，再由∠P=60°，可判定△PAB为等边三角形，进而得到AB=PA=8，连接OA，OB，由切线性质可得∠PAO＝∠PBO＝90°，再由四边形内角和即可求出∠AOB的度数.
解：∵PA，PB分别切⊙O于点A、B，
∴PA＝PB，
∵∠P＝60°，
∴△PAB是等边三角形，
∴AB＝PA＝PB，
∵PA＝8，
∴AB＝8．
如图，连接OA，OB，
则∠PAO＝∠PBO＝90°，
∴∠AOB＝360°﹣90°﹣90°﹣60°＝120°，
故答案为：8，120°．
练习册系列答案
阅读快车系列答案
相关题目
【题目】已知抛物线y＝x2﹣2x﹣3．
（1）抛物线与x的交点坐标是 ，顶点是 ．
（2）选取适当的数据填入下表．在直角坐标系中利用五点法画出此抛物线的图象．
X | … | … | |||||
y | … | … |
（3）结合函数图象，回答下题：
若抛物线上两点A（x1，y1），B（x2，y2）的横坐标满足x1＜x2＜1比较y1，y2的大小： ．当y＜0，自变量x的取值范围是 ．
