题目内容
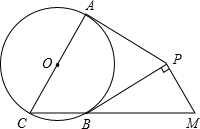 如图,PA、PB分别切⊙O于A、B,AC是⊙O的直径,过P作PM⊥BP交CB的延长线于M
如图,PA、PB分别切⊙O于A、B,AC是⊙O的直径,过P作PM⊥BP交CB的延长线于M(1)求证:∠C=∠M
(2)若cos∠C=
| 2 | 3 |
分析:(1)如图,连接OB、OP,构造平行线MP∥OB,所以由平行线的性质,等腰△OBC的性质以及等量代换证得结论;
(2)设⊙O的半径为R.如图,连接AB.根据垂径定理、圆周角定理以及(1)中的MP∥OB推知四边形OBMP是平行四边形.则对边OB=PM=R,通过解直角△ABC和直角△BPM分别求得线段BC=
R、BM=
R,然后结合已知条件知BC+BM=3.
(2)设⊙O的半径为R.如图,连接AB.根据垂径定理、圆周角定理以及(1)中的MP∥OB推知四边形OBMP是平行四边形.则对边OB=PM=R,通过解直角△ABC和直角△BPM分别求得线段BC=
| 4 |
| 3 |
| 3 |
| 2 |
解答: (1)证明,如图,连接OB、OP.∵PB是⊙O的切线,点B是切点,
(1)证明,如图,连接OB、OP.∵PB是⊙O的切线,点B是切点,
∴∠PBO=90°.
又∵PM⊥BP,
∴∠BPM=90°,
∴∠PBO=∠BPM,
∴MP∥OB,
∴∠M=∠OBC,
∵OB=OC,
∴∠OBC=∠C,
∴∠C=∠M;
(2)如图,连接AB,则OP⊥AB,CB⊥AB.
∴OP∥CM.
又∵MP∥OB,
∴四边形OBMP是平行四边形.
设⊙O的半径为R,则MP=OB=R.
∵cos∠C=
=
,
∴BC=
R.
∴cos∠M=cos∠C=
=
,
∴BM=
R,
∴
R+
R=3,
解得,R=
.
 (1)证明,如图,连接OB、OP.∵PB是⊙O的切线,点B是切点,
(1)证明,如图,连接OB、OP.∵PB是⊙O的切线,点B是切点,∴∠PBO=90°.
又∵PM⊥BP,
∴∠BPM=90°,
∴∠PBO=∠BPM,
∴MP∥OB,
∴∠M=∠OBC,
∵OB=OC,
∴∠OBC=∠C,
∴∠C=∠M;
(2)如图,连接AB,则OP⊥AB,CB⊥AB.
∴OP∥CM.
又∵MP∥OB,
∴四边形OBMP是平行四边形.
设⊙O的半径为R,则MP=OB=R.
∵cos∠C=
| BC |
| AC |
| 2 |
| 3 |
∴BC=
| 4 |
| 3 |
∴cos∠M=cos∠C=
| PM |
| BM |
| 2 |
| 3 |
∴BM=
| 3 |
| 2 |
∴
| 4 |
| 3 |
| 3 |
| 2 |
解得,R=
| 18 |
| 17 |
点评:本题考查了切线的性质,解直角三角形.解答(2)题时,借用了平行四边形的判定与性质.

练习册系列答案
相关题目
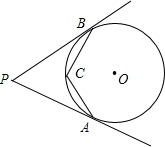 如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB=
如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB= 7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )
7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )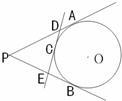 7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是
7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 (2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°.
(2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°. 如图,PA,PB分别切⊙O于点A和点B,C是
如图,PA,PB分别切⊙O于点A和点B,C是