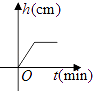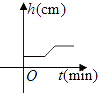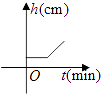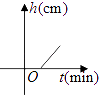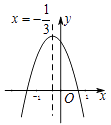题目内容
【题目】已知：甲、乙两车分别从相距300千米的A，B两地同时出发相向而行，甲到B地后立即返回，下图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．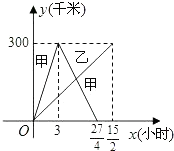
（1）请直接写出甲、乙两车离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数关系式，并标明自变量x的取值范围；
（2）它们在行驶的过程中有几次相遇？并求出每次相遇的时间．
【答案】
（1）解：甲由3小时到 
小时的速度是： 
=80千米/小时．
（2）解：由题意有两次相遇．
方法一：①当0≤x≤3时，100x+40x=300，解得 
，
②当 
时，（540﹣80x）+40x=300，解得x=6，
综上所述，两车第一次相遇时间为第 
小时，第二次相遇时间为第6小时．
方法二：设经过x小时两车首次相遇，
则40x+100x=300，解得 ，
设经过x小时两车第二次相遇，
则80（x﹣3）=40x，解得x=6．
综上所述，两车第一次相遇时间为第 小时，第二次相遇时间为第6小时．
【解析】（1）依图可知甲的图像是折线，y甲的函数关系式为分段函数，乙是线段；（2）根据第一次相遇时二者的路程和=300可列出方程100x+40x=300，第二次是甲追上乙，利用甲余下的路程加乙的路程和=300即（540﹣80x）+40x=300，解出方程即可解出.
名校课堂系列答案
【题目】A，B，C三名大学生竞选系学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，如表和图一：
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
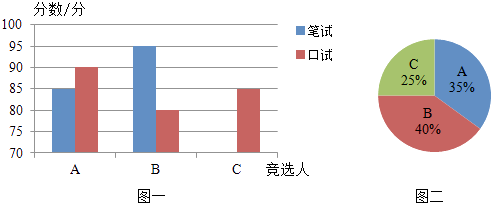
（1）请将表一和图一中的空缺部分补充完整．
（2）竞选的最后一个程序是由本系的300名学生进行投票，三位候选人的得票情况如图二（没有弃权票，每名学生只能推荐一个），请计算每人的得票数．
（3）若每票计1分，系里将笔试、口试、得票三项测试得分按4：3：3的比例确定个人成绩，请计算三位候选人的最后成绩，并根据成绩判断谁能当选．
