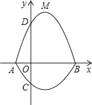
��Ŀ����
����Ŀ����ͼ��ʾ����ij�羰��������·��ʾ��ͼ������B��C��DΪ�羰�㣬EΪ����·�Ľ���㣬ͼ������Ϊ����Ӧ���ľ���(��λ��ǧ��)��һλ�οʹ�A����������2ǧ�ף�ʱ���ٶȲ���������ÿ������Ķ���ʱ���Ϊ![]() Сʱ��
Сʱ��

(1)��������·��A��D��C��E��A�����ص�A��ʱ��������4Сʱ����CE�ij���
(2)����ѧ�������A�������������ٶ��뾰��Ķ���ʱ�䱣�ֲ��䣬�������ʱ���ڿ����������㷵�ص�A��������Ϊ�����һ������·�ߣ�˵��������Ƶ����ɣ�
���𰸡���1��CE=0.2ǧ�ף���2������·��ӦΪA��D��C��E��B��E��A(��A��E��B��E��C��D��A)��������.
��������
��1����ϵʽΪ����·��=�ٶȡ�ʱ�䣬ע��ʱ��Ӧȥ������ʱ�䣮
��2�����ʱ���ڿ����������㷵�ص�A��Ӧѡ���ظ��߾������ڵ�·�ߣ�������Բ���CE��
��1����CE��Ϊxǧ�ף���2.2��1.4��x��1.2=2��(4��2��0.75)����ã�x=0.2��ǧ�ף���
��2��������·��ΪA��D��C��B��E��A����A��E��B��C��D��A����������ʱ��Ϊ��
��2.2��1.4��2��0.6��1.2����2��3��0.75=5.95��Сʱ����
������·��ΪA��D��C��E��B��E��A����A��E��B��E��C��D��A����������ʱ��Ϊ��
��2.2��1.4��0.2��0.6��2��1.2����2��3��0.75=5.35��Сʱ����
��Ϊ5.95��5.35�����Բ���·��ӦΪA��D��C��E��B��E��A����A��E��B��E��C��D��A����