Question

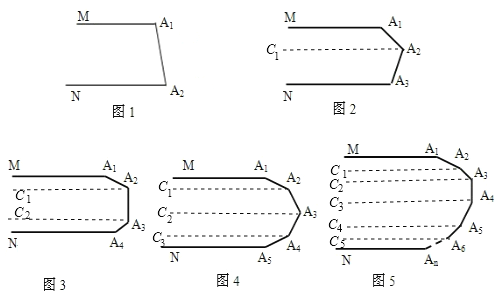
【题目】(1) 如图1，MA1∥NA2，则∠A1+∠A2=_________度．

如图2，MA1∥NA3，则∠A1+∠A2+∠A3=_________ 度．

如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4=_________度．

如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5=_________度．

如图5，MA1∥NAn，则∠A1+∠A2+∠A3+…+∠An=_________ 度．

(2) 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=80°，求∠BFD的度数.

【答案】（1） 180； 360； 540；720；180（n-1）；（2）140°.

【解析】试题分析：（1）首先过各点作MA 1 的平行线，由MA 1 ∥NA 2 ，可得各线平行，根据两直线平行，同旁内角互补，即可求得答案；

（2）由（1）中的规律可得∠ABE+∠E+∠CDE=360°，所以∠ABE+∠CDE=360°-80°=280°，又因为BF、DF平分∠ABE和∠CDE，所以∠FBE+∠FDE=140°，又因为四边形的内角和为360°，进而可得答案．

试题解析：（1）如图1，

∵MA 1 ∥NA 2 ，

∴∠A 1 +∠A 2 =180°．

如图2，过点A 2 作A 2 C 1 ∥A 1 M，

∵MA 1 ∥NA 3 ，

∴A 2 C 1 ∥A 1 M∥NA 3 ，

∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 3 =180°，

∴∠A 1 +∠A 2 +∠A 3 =360°．

如图3，过点A 2 作A 2 C 1 ∥A 1 M，过点A 3 作A 3 C 2 ∥A 1 M，

∵MA 1 ∥NA 3 ，

∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ，

∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°，∠C 2 A 3 A 4 +∠A 4 =180°，

∴∠A 1 +∠A 2 +∠A 3 +∠A 4 =540°．

如图4，过点A 2 作A 2 C 1 ∥A 1 M，过点A 3 作A 3 C 2 ∥A 1 M，

∵MA 1 ∥NA 3 ，

∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ，

∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°，∠C 2 A 3 A 4 +∠A 3 A 4 C 3 =180°，∠C 3 A 4 A 5 +∠A 5 =180°，

∴∠A 1 +∠A 2 +∠A 3 +∠A 4 +∠A 5 =720°；

从上述结论中你发现了规律：如图5，MA 1 ∥NA n ，则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180（n-1）度，

故答案为：180，360，540，720，180（n-1）；

（2）由（1）可得∠ABE+∠E+∠CDE=360°，

∵∠E=80°，

∴∠ABE+∠CDE=360°-80°=280°，

又∵BF、DF平分∠ABE和∠CDE，

∴∠FBE+∠FDE=140°，

∵∠FBE+∠E+∠FDE+∠BFD=360°，

∴∠BFD=360°-80°-140°=140°．

【点睛】本题考查了平行线的性质：两直线平行，同旁内角互补、四边形的内角和是360°，解题的关键是，（1）小题正确添加辅助线，发现规律：MA 1 ∥NA n ，则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180（n-1）度；（2）小题能应用（1）中发现的规律.

【题型】解答题
【结束】
28

【题目】已知如图1，线段AB、CD相交于点O，连结AC、BD，我们把形如图1的图形称之为“8字形”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥聪明才智，解决以下问题：

(1)在图1中，请写出∠A、∠B、∠C、∠D之间的数量关系，并说明理由；

(2)仔细观察，在图2中“8字形”的个数有 个；

(3)在图2中，若∠B＝76°，∠C＝80°，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N利用(1)的结论，试求∠P的度数；

(4)在图3中，如果∠B和∠C为任意角，并且AP和DP分别是∠CAB和∠BDC的三等分线，即∠PAO＝∠CAO， ∠BDP＝∠BOD，那么∠P与∠C、∠B之间存在的数量关系是 （直接写出结论即可）．

Answer 1

【答案】(1) ∠A+∠C=∠B+∠D；证明见解析；（2）6；（3）78°；（4）∠P=

【解析】试题分析：（1）根据对顶角相等和三角形内角和定理可得解；

（2）根据“8字形”的结构特点，根据交点写出“8字形”的三角形，然后确定即可；

（3）在图2中，由∠C=80°，∠B=76°，可求∠P的度数；

（4）由（3）中的结论可得解.

试题解析：（1）在△AOC中，∠AOC=180°-∠A-∠C，

在△DOB中，∠BOD=180°-∠D-∠B，

∵∠AOC=∠BOD

∴180°-∠A-∠C=180°-∠D-∠B

∴∠A+∠C=∠B+∠D

（2）交点有点M、N各有1个，交点O有4个，所以，“8字形”图形共有6个；

（3）∵∠B＝76°，∠C＝80°，

∴∠OAC+80°=∠ODB+76°，

∴∠ODB-∠OAC =4°，

∵AP、DP分别是∠CAO、∠BDO的角平分线

∴∠CAM=∠CAO,∠PDO=∠BDO

又∵∠CAM+∠C=∠PDO+∠P

∴∠P=∠CAM+∠C-∠PDO= (∠CAO-∠BDO)+∠C=-2°+80°=78°

（4）由（3）可知∠P=∠CAM+∠C-∠PDO，

当AP和DP分别是∠CAB和∠BDC的三等分线时，则有

∠CAM=∠CAO,∠PDO=∠BDO

∴∠P= (∠CAO-∠BDO)+∠C,

又∵由（3）知∠CAO-∠BDO=∠B-∠C

∴∠P=∠B-∠C+∠C=∠B+∠C