题目内容
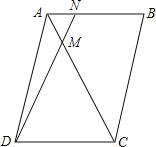
【题目】如图,四边形ABCD是平行四边形,点N是AB上一点,且BN=2AN,AC、DN相交于点M,则S△ADM:S四边形CMNB的值为( )
A.3:11 B.1:3 C.1:9 D.3:10
【答案】A
【解析】
试题分析:首先利用平行四边形的性质可证明:△AMN∽△CMD,利用相似三角形的性质:面积比等于相似比的平方即可求出S△ADM:S四边形CMNB的值.
解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∵△AMN∽△CMD,
∴AN:DC=AM:CM,
∵BN=2AN,
∴AN:DC=1:3,
∴S△AMN:S△DMC=1:9,
∵S△AMN:S△AMD=1:3,
∴S△ADM:S△DMC=1:3,
又∵S△ADC=S△ABC,
∴S△ADM:S四边形CMNB=3:11,
故选A.

练习册系列答案
相关题目