题目内容
∠A,∠B,∠C是△ABC的三个内角,下列各式成立的是
- A.sin
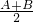 =sin
=sin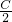
- B.cos
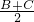 =cos
=cos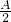
- C.tan
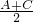 =tan
=tan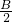
- D.sin
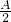 =cos
=cos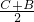
D
分析:根据锐角三角函数的概念,可以证明:若α+β=90°,则sinα=cosβ,tanα•tanβ=1.
解答:∵∠A,∠B,∠C是△ABC的三个内角,
∴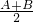 +
+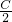 =90°,
=90°,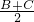 +
+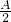 =90°,
=90°,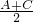 +
+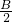 =90°.
=90°.
A、应是sin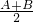 =cos
=cos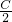 .错误;
.错误;
B、应是cos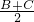 =sin
=sin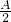 .错误;
.错误;
C、应是tan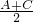 =
=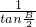 .错误;
.错误;
D、是sin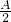 =cos
=cos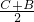 .正确;
.正确;
故选D.
点评:本题考查的是互余两角的三角函数的关系.
分析:根据锐角三角函数的概念,可以证明:若α+β=90°,则sinα=cosβ,tanα•tanβ=1.
解答:∵∠A,∠B,∠C是△ABC的三个内角,
∴
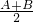 +
+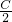 =90°,
=90°,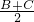 +
+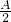 =90°,
=90°,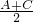 +
+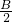 =90°.
=90°.A、应是sin
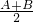 =cos
=cos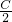 .错误;
.错误;B、应是cos
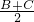 =sin
=sin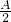 .错误;
.错误;C、应是tan
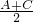 =
=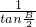 .错误;
.错误;D、是sin
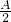 =cos
=cos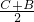 .正确;
.正确;故选D.
点评:本题考查的是互余两角的三角函数的关系.

练习册系列答案
相关题目
一组数据由五个正整数组成,中位数是3,且唯一众数是7,则这五个正整数的平均数是( )
| A、4 | B、5 | C、6 | D、8 |
圆锥的底面直径是8,母线长为12,则这个圆锥的侧面展开图的圆心角是( )
| A、60° | B、120° | C、150° | D、180° |
 4、如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠COB的补角是
4、如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠COB的补角是