题目内容
【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC 
(1)线段BC的长等于;
(2)请在图中按下列要求逐一操作,并回答问题: 以点为圆心,以线段的长为半径画弧,与射线BA交于点D,使线段OD的长等于 ![]()
(3)连OD,在OD上画出点P,使OP的长等于 ![]() ,请写出画法,并说明理由.
,请写出画法,并说明理由.
【答案】
(1)![]()
(2)A;BC
(3)解:∵OD= ![]() ,OP=
,OP= ![]() ,OC=OA+AC=3,OA=2,
,OC=OA+AC=3,OA=2,
∴ ![]() .
.
故作法如下:
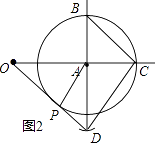
连接CD,过点A作AP∥CD交OD于点P,P点即是所要找的点.
依此画出图形,如图2所示.
【解析】解:(1)在Rt△BAC中,AB=AC=1,∠BAC=90°, ∴BC= ![]() =
= ![]() .
.
故答案为: ![]() .
.
2)在Rt△OAD中,OA=2,OD= ![]() ,∠OAD=90°,
,∠OAD=90°,
∴AD= ![]() =
= ![]() =BC.
=BC.
∴以点A为圆心,以线段BC的长为半径画弧,与射线BA交于点D,使线段OD的长等于 ![]() .
.
依此画出图形,如图1所示.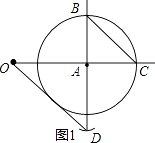
故答案为:A;BC.
(1)由圆的半径为1,可得出AB=AC=1,结合勾股定理即可得出结论;(2)结合勾股定理求出AD的长度,从而找出点D的位置,根据画图的步骤,完成图形即可;(3)根据线段的三等分点的画法,结合OA=2AC,即可得出结论.

 阅读快车系列答案
阅读快车系列答案【题目】已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变量和对应函数值如表:
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y2>y1时,自变量x的取值范围是( )
A.x<﹣1
B.x>4
C.﹣1<x<4
D.x<﹣1或x>4
【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数; 
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?