题目内容
已知α是锐角，且2cosα=1，则α=分析：根据特殊角度的三角函数值求解．
解答：解：（1）α是锐角，且2cosα=1，
∴cosα=
，
∴α=60°；
（2）tan（α+15°）=1．
∴α+15°=45°，∴α=30°．
∴tanα=tan30°=
．
∴cosα=
| 1 |
| 2 |
∴α=60°；
（2）tan（α+15°）=1．
∴α+15°=45°，∴α=30°．
∴tanα=tan30°=
| ||
| 3 |
点评：熟记特殊角的三角函数值是解题的关键．
练习册系列答案
相关题目
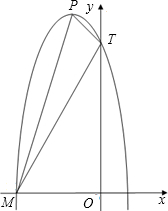如图，已知抛物线y=-3x2-（2c-b）x+a2，其中a、b、c是一个直角三角形的三边的长，且a＜b＜c，又知这个三角形两锐角的正弦值分别是方程25x2-35x+12=0的两个根．
如图，已知抛物线y=-3x2-（2c-b）x+a2，其中a、b、c是一个直角三角形的三边的长，且a＜b＜c，又知这个三角形两锐角的正弦值分别是方程25x2-35x+12=0的两个根．
