��Ŀ����
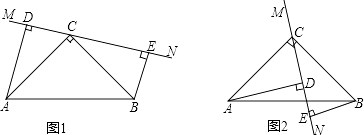
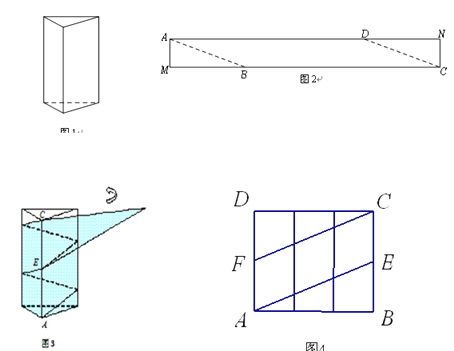
����Ŀ����ͼ1��һ����������װ�У����ĵ����DZ߳�Ϊ10cm���������Σ��������涼�Ǿ��Σ��ֽ���Ϊ15cm�IJ�ɫ����ֽ��AMCN�ü���һ��ƽ���ı���ABCD����ͼ2����Ȼ��������ƽ���ı���ֽ������ͼ3�ķ�ʽ�������������װ�еIJ�����а�����Ҫ�����ʱû���ص����֣���ֽ���ڲ��������Ȧ�����ý������������װ�еIJ���ȫ������������ͼ3�У����������ع���A�IJ���������õ���ͼ4�IJ���չ��ͼ.Ϊ�˵õ��ü��ĽǶ�,���ǿ��Ը���չ��ͼƴ�ӳ�����������ƽ���ı��ν����о�.
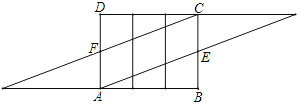
��1������ͼ4�л���ƴ�Ӻ����������ƽ���ı��Σ�
��2������ͼ2�У�����ü��ĽǶȣ�����ABM�Ķ�����.
���𰸡���1����ͼ����������2����ABM=30�㣮
����������������1����ͼ4�еġ�ABE����ƽ��30cm����CDF����ƽ��30cm��ƴ����ͼ�е�ƽ���ı��Σ���ƽ���ı��μ�Ϊͼ2�е��ı���ABCD��
��2���������������AB=30cm����ֽ���Ŀ�Ϊ15cm���������Ǻ�����á�AMB=30�㣮
�����������1����ͼ��
��2����ͼ2�İ�������֪��AB�ij������������ĵױ��ܳ�����AB=30��
�� ֽ����Ϊ15���� sin��ABM =![]() �����AMB=30�㣮
�����AMB=30�㣮

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�