题目内容
从-1,1,2这三个数中,任取两个不同的数作为一次函数y=kx+b的系数k,b,则一次函数y=kx+b的图象不经过第四象限的概率是( )
分析:先列表展示k、b的取值共有6种等可能的结果,再根据一次函数的性质得到一次函数y=kx+b的图象不经过第四象限时有k>0,b≥0,则满足条件的k、b的取值有(1,2),(2,1),然后根据概率的定义即可得到一次函数y=kx+b的图象不经过第四象限的概率.
解答:解:列表 ,如图,
,如图,
k、b的取值共有6种等可能的结果;
而一次函数y=kx+b的图象不经过第四象限,则k>0,b≥0,
∴满足条件的k、b的取值有(1,2),(2,1),
∴一次函数y=kx+b的图象不经过第四象限的概率=
=
.
故选C.
 ,如图,
,如图,k、b的取值共有6种等可能的结果;
而一次函数y=kx+b的图象不经过第四象限,则k>0,b≥0,
∴满足条件的k、b的取值有(1,2),(2,1),
∴一次函数y=kx+b的图象不经过第四象限的概率=
| 2 |
| 6 |
| 1 |
| 3 |
故选C.
点评:本题考查了利用列表法与树状图法求概率的方法:先列表展示所有等可能的结果数n,再找出某事件发生的结果数m,然后根据概率的定义计算出这个事件的概率=
.也考查了一次函数的性质.
| m |
| n |

练习册系列答案
相关题目
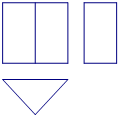 分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图所示的平面图形,那么这个几何体是( )
分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图所示的平面图形,那么这个几何体是( )