Question

【题目】如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．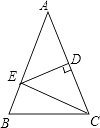
（1）求∠BEC的度数．
（2）若CE=5，求BC的长．

Answer 1

【答案】
（1）解：∵DE垂直平分AC，

∴CE=AE，

∴∠ECD=∠A=36°，

∴∠BEC=∠A+∠ECD=36°+36°=72°

（2）解：∵AB=AC，∠A=36°，

∴∠B=∠ACB=72°，

∴∠BEC=∠A+∠ECD=72°，

∴∠BEC=∠B，

∴BC=EC=5

【解析】（1）ED是AC的垂直平分线，可得AE=EC；∠A=∠ACE；已知∠A=36，可求∠ACE，再根据三角形外角的性质即可求解；（2）根据等腰三角形性质和三角形内角和定理求出∠B=∠ACB=72°，求出∠BEC=∠B，推出BC=CE即可．