题目内容
将两块全等的三角板ABC和DEC按如图所示的位置放置.∠B=60°,AC=2,若三角板ABC绕点C沿逆时针方向旋转,使点E恰好落在斜边AB上,则点A运动路径的长度为( )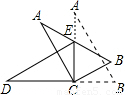
A.
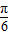
B.
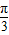
C.
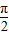
D.

【答案】分析:根据题意确定△CEB为等边三角形,从而得出∠ECB的度数,结合AC=2,代入弧长运算公式即可得出答案.
解答:解:∵△ABC≌△DEC,
∴CE=CB,
又∵∠B=60°,
∴△CEB为等边三角形,
∴∠ECB=60°,
∴∠ACE=30°,
则A运动路径的长度=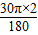 =
=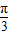 .
.
故选B.
点评:本题考查了弧长的计算,解答本题的关键是根据题意判断△CEB为等边三角形,另外要求同学们熟练掌握弧长的计算公式.
解答:解:∵△ABC≌△DEC,
∴CE=CB,
又∵∠B=60°,
∴△CEB为等边三角形,
∴∠ECB=60°,
∴∠ACE=30°,
则A运动路径的长度=
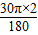 =
=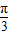 .
.故选B.
点评:本题考查了弧长的计算,解答本题的关键是根据题意判断△CEB为等边三角形,另外要求同学们熟练掌握弧长的计算公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 将两块全等的三角板ABC和DEC按如图所示的位置放置.∠B=60°,AC=2,若三角板ABC绕点C沿逆时针方向旋转,使点E恰好落在斜边AB上,则点A运动路径的长度为( )
将两块全等的三角板ABC和DEC按如图所示的位置放置.∠B=60°,AC=2,若三角板ABC绕点C沿逆时针方向旋转,使点E恰好落在斜边AB上,则点A运动路径的长度为( )
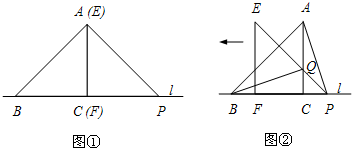
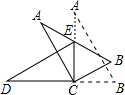
 与AB的交点,点Q是
与AB的交点,点Q是 与BC的交点,求证:
与BC的交点,求证: =
= ;
; ,则CQ等于多少?
,则CQ等于多少? 绕点C顺时针旋转到△
绕点C顺时针旋转到△ (如图3),点
(如图3),点 与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段 之间存在一个怎样的数量关系?.
之间存在一个怎样的数量关系?.