题目内容
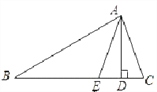
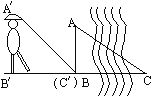
【题目】如图所示，传说在19世纪初，一位将军率领部队在一河边与敌军激战，为使炮弹准确地落在河对岸的敌军阵地，将军站在河这岸，将帽檐压低，使视线沿着帽檐恰好落在河对岸的边线上，然后他向后退(保证B′、B、C在一条直线上)，一直退到视线落在河这岸的边线上为止，这时，他后退的距离就等于河宽，这是为什么？请给予证明．
【答案】证明见解析.
【解析】分析:根据奖将军的身高不变可得AB=
,视线方向不变可得∠A=
,然后利用“边角边”证明△ABC≌△
,根据全等三角形对应边相等可得BC=
,从而得到将军后退的距离便是河的宽度.
本题解析：
根据题意，∠ABC=∠ABC =90°，
在△ABC和△ABC中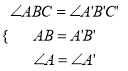
，∴△ABC≌△ABC，∴BC=BC.
他后退的距离就等于河宽.
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
