题目内容
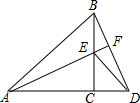 如图,△ACB和△ECD中,AC=BC,CE=CD,BC⊥AD,A、C、D三点在同一直线上,连接BD、AE,并延长交BD于F.
如图,△ACB和△ECD中,AC=BC,CE=CD,BC⊥AD,A、C、D三点在同一直线上,连接BD、AE,并延长交BD于F.(1)求证:△ACE≌△BCD;
(2)直线AF与BD有怎样的位置关系?并说明理由.
分析:(1)由全等三角形的判定定理SAS证得结论;
(2)由△ACE≌△BCD推出∠EAC=∠DBC,根据三角形的内角和定理求出∠EAC+∠AEC=90°,求出∠DBC+∠BEF=90°,根据三角形的内角和定理求出∠BFE=90°,根据垂直定义推出即可.
(2)由△ACE≌△BCD推出∠EAC=∠DBC,根据三角形的内角和定理求出∠EAC+∠AEC=90°,求出∠DBC+∠BEF=90°,根据三角形的内角和定理求出∠BFE=90°,根据垂直定义推出即可.
解答: (1)证明:如图,∵BC⊥AD,
(1)证明:如图,∵BC⊥AD,
∴∠ACE=∠BCD=90°,
∴在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS);
(2)解:直线AF与BD垂直.理由如下:
∵由(1)知,△ACE≌△BCD,
∴∠EAC=∠DBC,
∵∠ACB=90°,
∴∠EAC+∠AEC=90°,
∵∠AEC=∠BEF,
∴∠DBC+∠BEF=90°,
∴∠BFE=180°-90°=90°,
∴AF⊥BD.
 (1)证明:如图,∵BC⊥AD,
(1)证明:如图,∵BC⊥AD,∴∠ACE=∠BCD=90°,
∴在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS);
(2)解:直线AF与BD垂直.理由如下:
∵由(1)知,△ACE≌△BCD,
∴∠EAC=∠DBC,
∵∠ACB=90°,
∴∠EAC+∠AEC=90°,
∵∠AEC=∠BEF,
∴∠DBC+∠BEF=90°,
∴∠BFE=180°-90°=90°,
∴AF⊥BD.
点评:本题考查了全等三角形的性质和判定,三角形的内角和定理,对顶角相等,垂直定义等知识点的综合运用,关键是推出∠BFE=90°,全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应角相等.

练习册系列答案
相关题目
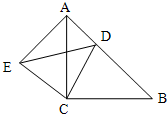 21、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
21、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证: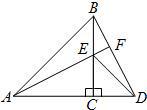 14、如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
14、如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.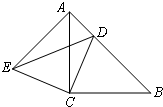 16、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
16、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.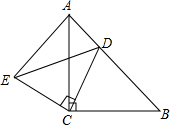 如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.
如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.