题目内容
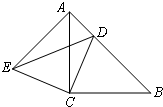 16、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
16、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.求证:AE=BD.
分析:要证AE=BD,经过观察分析我们可以将这两条线段放在三角形ACE和三角形BCD中,证其全等即可.首先我们根据△ACB和△ECD都是等腰直角三角形,得出两对对应边的相等,然后又根据∠ACB=∠ECD,都减去中间的公共角ACD再得一对对应角的相等,根据SAS证三角形ACE和三角形BCD的全等,最后根据全等三角形的对应边相等即可得证.
解答: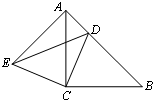 解:证明:∵△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
解:证明:∵△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
∴EC=CD,AC=CB,
∠ACB-∠ACD=∠ECD-∠ACD.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD.
 解:证明:∵△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
解:证明:∵△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,∴EC=CD,AC=CB,
∠ACB-∠ACD=∠ECD-∠ACD.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD.
点评:解此题时要充分利用等腰直角三角形的性质,熟练掌握三角形全等的证明以及对全等三角形的性质的理解掌握.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
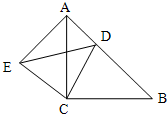 21、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
21、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证: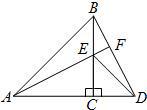 14、如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
14、如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.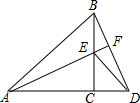 如图,△ACB和△ECD中,AC=BC,CE=CD,BC⊥AD,A、C、D三点在同一直线上,连接BD、AE,并延长交BD于F.
如图,△ACB和△ECD中,AC=BC,CE=CD,BC⊥AD,A、C、D三点在同一直线上,连接BD、AE,并延长交BD于F.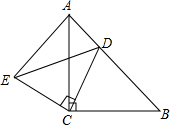 如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.
如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.