题目内容
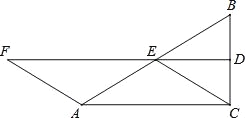
【题目】如图,△ABC中,∠ACB=90°,D、E分别是BC、BA的中点,连接DE,F在DE延长线上,且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
【答案】(1)证明参见解析;(2)30°.
【解析】
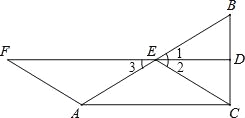
试题分析:(1)如下图:根据直角三角形斜边上的中线等于斜边的一半可得CE=AE=BE,从而得到AF=CE,再根据等腰三角形三线合一的性质可得∠1=∠2,根据等边对等角可得∠F=∠3,因为∠1=∠3,即可求出∠2=∠F,再根据同位角相等,两直线平行求出CE∥AF,然后利用一组对边平行且相等的四边形是平行四边形求证;(2)根据菱形的四条边都相等可得AC=CE,然后求出AC=CE=AE,从而得到△AEC是等边三角形,再根据等边三角形的每一个角都是60°求出∠CAE=60°,然后根据直角三角形两锐角互余解答.
试题解析:(1)∵∠ACB=90°,E是BA的中点,直角三角形斜边上的中线等于斜边的一半,∴CE=AE=BE,∵AF=AE,∴AF=CE,在△BEC中,∵BE=CE且D是BC的中点,∴ED是等腰△BEC底边上的中线,∴ED也是等腰△BEC的顶角平分线,∴∠1=∠2,∵AF=AE,∴∠F=∠3,∵∠1=∠3,∴∠2=∠F,∴CE∥AF,又∵CE=AF,∴四边形ACEF是平行四边形(一组对边平行且相等的四边形是平行四边形);(2)∵四边形ACEF是菱形,∴AC=CE,由(1)知,AE=CE,∴AC=CE=AE,∴△AEC是等边三角形,∴∠CAE=60°,在Rt△ABC中,∠B=90°﹣∠CAE=90°﹣60°=30°.故∠B=30°.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目