题目内容
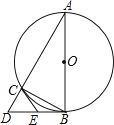
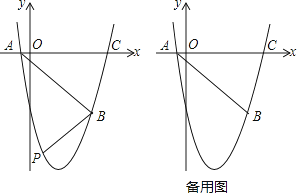
【题目】如图1,在直角坐标系xOy中,点A在y轴上,点B,点C在x轴上,点C在点B的右侧,OA=2OB=2BC=2.
(1)点C的坐标是 ;
(2)点P是x轴上一点,点P到AC的距离等于AC的长度,求点P的坐标;
(3)如图2,点D是AC上一点,∠CBD=∠ABO,连接OD,在AB上是否存在一点Q,使QB=AB﹣OD,若存在,求点Q与点D的横坐标之和,若不存在,请说明理由.

【答案】(1)(2,0);(2)P(﹣2,0)或(6,0);(3)点Q与点D的横坐标之和为2或![]() .
.
【解析】
(1)根据2OB=2BC=2,可得OB=BC=1,进而可求得OC=OB+BC=2,所以C(2,0),
(2)如图1,
根据OA=2,可得A(0,2),根据C(2,0)由勾股定理可得:AC=2![]() ,
,
过点P作PD⊥AC于D,根据点P到AC的距离等于AC的长度,可得DP=AC=2![]() ,
,
再根据∠PDC=∠AOC,∠PCD=∠ACO,可证:△PCD∽△ACO,根据相似三角形的性质可得:
![]() 即
即![]() ,解得PC=4,进而求得:OP=PC+OC=4+2=6,所以P(6,0)或OP=PC﹣OC=4﹣2=2,即:P(﹣2,0)或(6,0),
,解得PC=4,进而求得:OP=PC+OC=4+2=6,所以P(6,0)或OP=PC﹣OC=4﹣2=2,即:P(﹣2,0)或(6,0),
(3)如图2,延长DB交y轴点E,可得∠DBC=∠OBE,
根据∠DBC=∠ABO,可得:∠OBC=∠OBA,根据OB⊥AE,可得OE=OA=2,求得E(0,﹣2),
根据OB=1,可得B(1,0),利用待定系数法求得:直线BD的解析式为y=2x﹣2①,
再根据A(0,2),C(2,0),可求得直线AC的解析式为y=﹣x+2②,联立①②解得,x=![]() ,y=
,y=![]() ,
,
求出点D(![]() ,
,![]() ),故OD=
),故OD=![]() ,根据A(0,2),B(1,0),可得直线AB的解析式为y=﹣2x+2,
,根据A(0,2),B(1,0),可得直线AB的解析式为y=﹣2x+2,
设点Q(m,﹣2m+2),由B(1,0),利用勾股定理可得:BQ=![]() =
=![]() |m﹣1|,由A(0,2),B(1,0),可求得:AB=
|m﹣1|,由A(0,2),B(1,0),可求得:AB=![]() ,再根据QB=AB﹣OD,可得
,再根据QB=AB﹣OD,可得![]() |m﹣1|=
|m﹣1|=![]() ﹣
﹣![]() =
=![]() ,
,
解得:m=![]() 或m=
或m=![]() ,进而可得:Q(
,进而可得:Q(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),所以点Q与点D的横坐标之和为
),所以点Q与点D的横坐标之和为![]() +
+![]() =2或
=2或![]() +
+![]() =
=![]() .
.
解:(1)∵2OB=2BC=2,
∴OB=BC=1,
∴OC=OB+BC=2,
∴C(2,0),
故答案为:(2,0),
(2)如图1,
∵OA=2,
∴A(0,2),
∵C(2,0),
∴AC=2![]() ,
,
过点P作PD⊥AC于D,
∵点P到AC的距离等于AC的长度,
∴DP=AC=2![]() ,
,
∵∠PDC=∠AOC,∠PCD=∠ACO,
∴△PCD∽△ACO,
∴![]() ,
,
∴![]()
∴PC=4,
∴OP=PC+OC=4+2=6,
∴P(6,0)或OP=PC﹣OC=4﹣2=2,
∴P(﹣2,0),
即:P(﹣2,0)或(6,0),
(3)存在,理由:如图2,
延长DB交y轴点E,
∴∠DBC=∠OBE,
∵∠DBC=∠ABO,
∴∠OBC=∠OBA,
∵OB⊥AE,
∴OE=OA=2,
∴E(0,﹣2),
∵OB=1,
∴B(1,0),
∴直线BD的解析式为y=2x﹣2①,
∵A(0,2),C(2,0),
∴直线AC的解析式为y=﹣x+2②,
联立①②解得,x=![]() ,y=
,y=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴OD=![]() ,
,
∵A(0,2),B(1,0),
∴直线AB的解析式为y=﹣2x+2,
设点Q(m,﹣2m+2),
∵B(1,0),
∴BQ=![]() =
=![]() |m﹣1|,
|m﹣1|,
∵A(0,2),B(1,0),
∴AB=![]() ,
,
∵QB=AB﹣OD,
∴![]() |m﹣1|=
|m﹣1|=![]() ﹣
﹣![]() =
=![]() ,
,
∴m=![]() 或m=
或m=![]() ,
,
∴Q(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),
),
∴点Q与点D的横坐标之和为![]() +
+![]() =2或
=2或![]() +
+![]() =
=![]() .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题: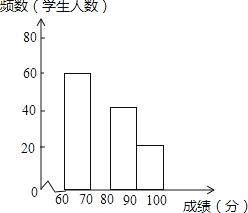
(1)在表中的频数分布表中,m= , n= .
成绩 | 频数 | 频率 |
60≤x<70 | 60 | 0.30 |
70≤x<80 | m | 0.40 |
80≤x<90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
(2)请补全图中的频数分布直方图.
(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?