题目内容
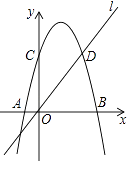
【题目】如图,已知抛物线 ![]() (其中
(其中 ![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点 ![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
【答案】
(1)
解:求得点A(-1,0)、B(b,0)、C(0,![]() b),
b),
易得∠ACB=90°,由△AOC∽△COB可得b1=4,b2=0(舍去),
∴y=![]() x2+
x2+![]() x+2.
x+2.
(2)
解:易证∠ACO=∠CBO,∠MNB=∠MBN,所以∠BED=∠CBN,
连结CN, 由勾股定理得CN=![]() ,BC=
,BC=![]() ,BN=
,BN=![]() ,
,
由勾股定理逆定理证得∠CNB=90°,从而得tan∠BED =tan∠CBN =![]() ,
,
然后解Rt△BED可得DE=![]() ,
,
∴点E坐标为(![]() ,
,![]() ) 或(
) 或(![]() ,
,![]() ).
).
【解析】(1)根据△AOC∽△COB求得b的值,在利用待定系数法解出解析式即可.
(2) 由勾股定理得CN=![]() ,BC=
,BC=![]() ,BN=
,BN=![]() ,由勾股定理逆定理证得∠CNB=90°,从而得tan∠BED =tan∠CBN =
,由勾股定理逆定理证得∠CNB=90°,从而得tan∠BED =tan∠CBN =![]() , 然后解Rt△BED解出DE的长即可得出点E坐标.
, 然后解Rt△BED解出DE的长即可得出点E坐标.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

练习册系列答案
相关题目