题目内容
【题目】随着教育信息化的发展,学生的学习方式日益增多,教师为了指导学生有效利用网络进行学习,对学生进行了随机问卷调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题: 
(1)本次接受问卷调查的学生共有人,在扇形统计图中“D“选项所占的百分比为;
(2)扇形统计图中,“B”选项所对应扇形圆心角为度;
(3)请补全条形统计图;
(4)若该校共有1200名学生,请您估计该校学生课外利用网络学习的时间在“A”选项的有多少人?
【答案】
(1)100;10%
(2)72
(3)解:因为,A选项的人数=100﹣20﹣50﹣10=20(人),则,条形统计图补全如下图所示:
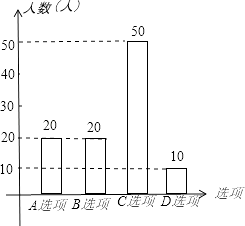
接受调查学生条形统计图
(4)解:因为,A选项所占的百分比为20%,
所以,1200×20%=240(人)
即,课外利用网络学习的时间在“A”选项的有240人
【解析】解:(1)因为,图(1)、图(2)中已知C选项的百分比是50%,人数是50,
所以,本次接受问卷调查的学生=50÷50%=100(人)
又,D选项的人数是20
所以,D选项的百分比= ![]() %=20%
%=20%
故答案为100,10%,
2)因为,B选项的人数为20,
所以,B选项的百分比=20÷100=20%,
故,B选项所对应扇形圆心角=360°×20%=72°.
故答案为72
由条形统计图与扇形统计图获得的数据:(1)因为图(1)、图(2)中已知C选项的百分比与人数,由C选项的百分比= ![]() ×100%求解(2)先求出B选项的百分比,再利用扇形统计图的圆心角的度数=360°×B选项的百分比求解(3)由(1)所得总人数求出B选项的人数即可作图(4)先求出A选项的百分比即可求得.此题是条形统计图,是常规题型,考查的是概率与统计中条形统计图、扇形统计图、利用样本估计总体等基础知识点
×100%求解(2)先求出B选项的百分比,再利用扇形统计图的圆心角的度数=360°×B选项的百分比求解(3)由(1)所得总人数求出B选项的人数即可作图(4)先求出A选项的百分比即可求得.此题是条形统计图,是常规题型,考查的是概率与统计中条形统计图、扇形统计图、利用样本估计总体等基础知识点

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别 | 分组 | 频数 | 频率 |
1 | 50≤x<60 | 9 | 0.18 |
2 | 60≤x<70 | a | |
3 | 70≤x<80 | 20 | 0.40 |
4 | 80≤x<90 | 0.08 | |
5 | 90≤x≤100 | 2 | b |
合计 |
请根据以上频率分布表和频率分布直方图,回答下列问题: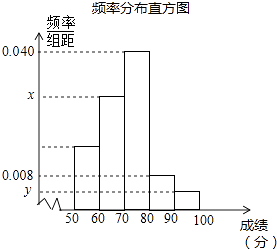
(1)求出a、b、x、y的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)