题目内容
课题学习●探究:
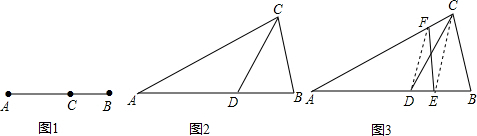
(1)在图1中,已知线段AB,CD,其中点分别为E,F.
①若A(-1,0),B(3,0),则E点坐标为
②若C(-2,2),D(-2,-1),则F点坐标为
(2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的
代数式表示),并给出求解过程.
●归纳:
无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y) 时,
x=
●运用:
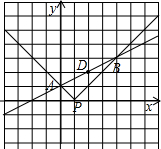
在图2中,y=|x-1|的图象x轴交于P点.一次函数y=kx+1与y=|x-1|的图象交点为A,B.
①求出交点A,B的坐标(用k表示);
②若D为AB中点,且PD垂直于AB时,请利用上面的结论求出k的值.

分析:(1)从在数轴上的两个特殊需要点的找到中点与端点坐标的关系,再到象限一般情况中点与端点的坐标关系.通过观察,从特殊到一般;再利用数形结合的思想,利用中点坐标公式求解.
(2)求出线段中点坐标分别是两个端点纵、横坐标的平均值.绝对值函数的图象画法,Y的值都是非负数.
(2)求出线段中点坐标分别是两个端点纵、横坐标的平均值.绝对值函数的图象画法,Y的值都是非负数.
解答:解:探究(1)①(1,0);②(-2,
);
(2)过点A,D,B三点分别作x轴的垂线,垂足分别为A′,D′,B′,则AA′∥BB′∥DD′.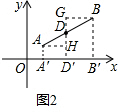
过A、B分别作直线DD'的垂线,垂足分别为H、G.
∴AH=BG,又AH=A′D′;BG=D′B′
∴A′D′=D′B′.x-a=c-x,x=
即D点的横坐标是
.
同理又HD=DG,d-y=y-b,y=
可得D点的纵坐标是
∴AB中点D的坐标为(
,
).
归纳:
,
●运用
,
或
,
或
,
∵AB⊥PD,p(1,0),A(0,1),B(
,
).
∴xp=xD=
=1,k=0.
| 1 |
| 2 |
(2)过点A,D,B三点分别作x轴的垂线,垂足分别为A′,D′,B′,则AA′∥BB′∥DD′.

过A、B分别作直线DD'的垂线,垂足分别为H、G.
|
∴AH=BG,又AH=A′D′;BG=D′B′
∴A′D′=D′B′.x-a=c-x,x=
| a+c |
| 2 |
即D点的横坐标是
| a+c |
| 2 |

同理又HD=DG,d-y=y-b,y=
| b+d |
| 2 |
可得D点的纵坐标是
| b+d |
| 2 |
∴AB中点D的坐标为(
| a+c |
| 2 |
| b+d |
| 2 |
归纳:
| a+c |
| 2 |
| b+d |
| 2 |
●运用
|
|
|
|
|
∵AB⊥PD,p(1,0),A(0,1),B(
| 2 |
| 1-k |
| 1+k |
| 1-k |
∴xp=xD=
| ||
| 2 |
点评:本题考查了一次函数的综合运用:从在数轴上的两个特殊需要点的找到中点与端点坐标的关系,再到象限一般情况中点与端点的坐标关系.通过观察,从特殊到一般;再利用数形结合的思想,利用中点坐标公式求解.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目