题目内容
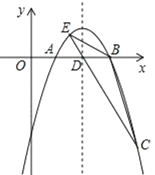
【题目】如图，二次函数
的图象与
轴交于
，
两点，并经过点
，对称轴交轴于点
，已知点坐标是
.
(1)求点和点的坐标.
(2)连接并延长
交抛物线于点
，连接
，
，求
的面积.
(3)抛物线上有一个动点
，与，两点构成
，是否存在
？若存在，请求出点的坐标；若不存在，请说明理由.
【答案】(1)
，
；(2)
；(3)存在，
或
或
或
.
【解析】
（1）利用待定系数法求出抛物线解析式，进而求出抛物线对称轴，求出点D的坐标，再令y=0，进而求出点B坐标；
（2）先利用待定系数法求出直线CD的解析式，进而求出点E的坐标，再求出点F的坐标，即可得出结论；
（3）先求出△DBC的面积，进而求出△ABP，求出点P的纵坐标，即可得出结论．
(1)二次函数
的图象经过点
，点
，
∴
∴
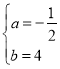
∴二次函数的解析式为
∴抛物线的对称轴为
∴
当
时，则
∴
(点
的横坐标)或
∴
(2)由(1)知，
∵
∴直线
的解析式为
①
由(1)知，二次函数的解析式为②
联立①②解得，
或
(点
的纵横坐标)
∴点
如图1，过点
作
轴交于
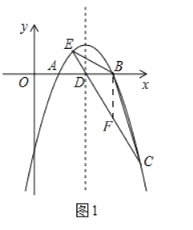
由(1)知，
∴
∴
(3)设点
的纵坐标为
，由(1)知，，
∵
∴
∵
∴
∵，
∴
∴
当
时，
，
或
，
∴或
当
时，
，
或
∴
或，即：或或或
练习册系列答案
相关题目
【题目】借鉴我们已有研究函数的经验，探索函数
的图象与性质，探究过程如下，请补充完整.
（1）自变量
的取值范围是全体实数，与
的几组对应值列表如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中，
，
；
（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出函数图象；
（3）观察函数图象：
①当方程
有且仅有两个不相等的实数根，根据函数图象直接写出
的取值范围为 ；
②在该平面直角坐标系中画出直线
的图象，根据图象直接写出该直线与函数
的交点横坐标为： （结果保留一位小数）.
