题目内容
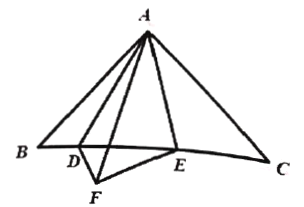
【题目】如图 ，在
中， 
，
，点
、
为 
边上两点， 将
、
分别沿
、
折叠，
、
两点重合于点
，若
，则的长为__________．
【答案】3
或2
【解析】
过点A作AG⊥BC，垂足为G，由等腰三角形的性质可求得AG=BG=GC=6，设BD=x，则DF=x，EF=7-x，然后在Rt△DEF中依据勾股定理列出关于x的方程，从而可求得DG的值，然后依据勾股定理可求得AD的值．
如图所示：过点A作AG⊥BC，垂足为G．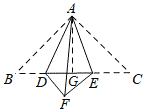
∵AB=AC=6
，∠BAC=90°，
∴BC=
=12．
∵AB=AC，AG⊥BC，
∴AG=BG=CG=6．
设BD=x，则EC=7-x．
由翻折的性质可知：∠B=∠DFA=∠C=∠AFE=45°，DB=DF，EF=EC．
∴DF=x，EF=7-x．
在Rt△DEF中，DE2=DF2+EF2，即25=x2+（7-x）2，解得：x=3或x=4．
当BD=3时，DG=3，AD=
当BD=4时，DG=2，AD=
∴AD的长为3 或2
故答案为：3 或2
智趣寒假作业云南科技出版社系列答案【题目】为了鼓励市民节约用水，某市水费实行分段计费制，每户每月用水量在规定用量及以下的部分收费标准相同，超出规定用量的部分收费标准相同．例如：若规定用量为10吨，每月用水量不超过10吨按1.5元/吨收费，超出10吨的部分按2元/吨收费，则某户居民一个月用水8吨，则应缴水费：8×1.5=12（元）；某户居民一个月用水13吨，则应缴水费：10×1.5+（13﹣10）×2=21（元）．
表是小明家1至4月份用水量和缴纳水费情况，根据表格提供的数据，回答：
月份 | 一 | 二 | 三 | 四 |
用水量（吨） | 6 | 7 | 12 | 15 |
水费（元） | 12 | 14 | 28 | 37 |
（1）该市规定用水量为 吨，规定用量内的收费标准是 元/吨，超过部分的收费标准是 元/吨．
（2）若小明家五月份用水20吨，则应缴水费 元．
（3）若小明家六月份应缴水费46元，则六月份他们家的用水量是多少吨？
